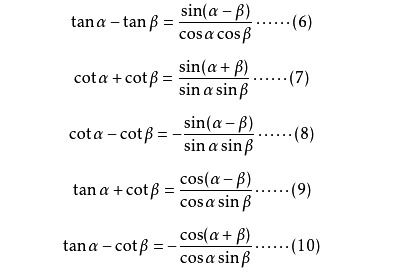余切函数的定义及公式

余切公式指的是什么

在数学中，三角函数是初等函数的重要组成部分，它们广泛应用于几何、物理、工程等领域。余切函数作为三角函数的一种，其定义、性质和公式在数学理论及实际应用中都占据重要地位。本文将从余切函数的定义、公式、性质及其在坐标系中的表示等多个维度，详细阐述余切公式的含义。

一、余切函数的定义

余切函数，通常记作cotθ，是三角函数的一种。在直角三角形中，一个锐角的余切定义为该角的相邻直角边与相对直角边的比值。假设在直角三角形ABC中，∠A是一个锐角，BC为∠A的对边，AC为∠A的邻边，AB为斜边。那么，∠A的余切cotA就等于AC（邻边）与BC（对边）的比值，即cotA = AC/BC = b/a。

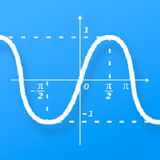
余切函数也可以用坐标系中的坐标来表示。在平面直角坐标系中，假设一个角θ的终边上除顶点外的任一点的横坐标为x，纵坐标为y（且y≠0），则该角的余切值cotθ等于该点的横坐标x与纵坐标y的比值，即cotθ = x/y。

二、余切函数的公式

余切函数的公式可以从多个角度推导和表示。

1. 直角三角形中的余切公式：

在直角三角形中，余切的定义直接给出了其公式，即cotA = 邻边/对边。这是余切函数最基础也是最重要的公式。

2. 坐标系中的余切公式：

在平面直角坐标系中，余切函数可以用终边上点的坐标来表示，即cotθ = x/y（其中y≠0）。这个公式揭示了余切函数与坐标系中点的位置之间的关系。

3. 与正切函数的关系：

余切函数与正切函数互为倒数关系，即cotθ = 1/tanθ（当tanθ≠0时）。这个关系使得余切函数可以通过正切函数的值来求解，反之亦然。

4. 与正弦、余弦函数的关系：

余切函数也可以用正弦和余弦函数的比值来表示，即cotθ = cosθ/sinθ（当sinθ≠0时）。这个公式揭示了余切函数与正弦、余弦函数之间的内在联系。

三、余切函数的性质

余切函数具有一些独特的性质，这些性质使得余切函数在数学和实际应用中具有重要的作用。

1. 周期性：

余切函数是周期函数，其周期为π。这意味着cot(θ + kπ) = cotθ，其中k是任意整数。这个性质使得余切函数在周期性的物理现象（如波动、振动等）中具有重要应用。

2. 奇偶性：

余切函数是奇函数，即cot(-θ) = -cotθ。这个性质使得余切函数在关于原点对称的图形和物理问题中具有特殊意义。

3. 单调性：

在(0, π)区间内，余切函数是单调递减的。这意味着当θ在这个区间内增大时，cotθ的值会减小。这个性质使得余切函数在比较角度大小时具有参考价值。

4. 渐近性：

当θ接近kπ（k为整数）时，cotθ的绝对值会趋于无穷大。这个性质揭示了余切函数在某些特殊点附近的行为特征。

四、余切函数在坐标系中的表示

在平面直角坐标系中，余切函数可以通过终边上点的坐标来表示。假设一个角θ的终边上除顶点外的任一点的横坐标为x，纵坐标为y（且y≠0），则该角的余切值cotθ等于该点的横坐标x与纵坐标y的比值，即cotθ = x/y。

这个表示方法使得余切函数与坐标系中的点建立了联系，从而可以通过几何图形来直观地理解余切函数的性质。例如，当θ在第一象限时，x和y都为正数，所以cotθ为正数；当θ在第二象限时，x为负数，y为正数，所以cotθ为负数；以此类推，可以得出cotθ在不同象限的符号规律。

五、余切函数的应用

余切函数在数学和实际应用中具有广泛的应用。

1. 几何应用：

在几何学中，余切函数可以用于求解直角三角形中的边长和角度问题。例如，在已知一个锐角和一条边长的情况下，可以利用余切函数求解另一条边长。

2. 物理应用：

在物理学中，余切函数常用于描述周期性的物理现象，如波动、振动等。此外，在力学、电磁学等领域