探索长方体的奇妙特征：全面了解它的独特之处

长方体的特征有哪些

长方体是日常生活中非常常见的一种几何体，它广泛应用于建筑、家具、包装等多个领域。那么，长方体究竟有哪些特征呢？下面我们就来详细探讨一下。

一、长方体的定义

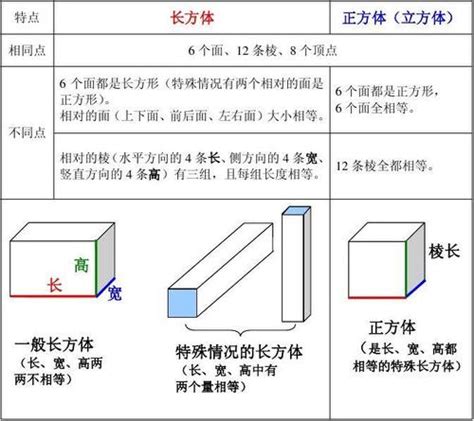
长方体是一种特殊的多面体，它由六个面组成，其中每一个面都是一个矩形。长方体的定义可以用以下几个条件来概括：

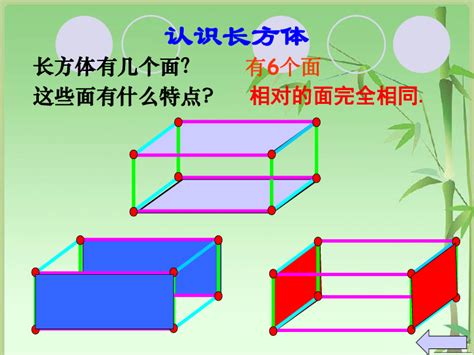
1. 有六个面，每个面都是矩形。

2. 相对的两个面完全相同，即前后面、左右面、上下面各自相同。

3. 有十二条棱，分别连接各个面的顶点。每四条棱互相平行且等长，分别是长方体的长、宽、高。

4. 有八个顶点，每个顶点都是三条棱的交点。

二、长方体的面

长方体的面是其最重要的特征之一。由于长方体的每一个面都是矩形，因此它具有矩形的所有性质，如对角线相等、对边平行且等长等。长方体的六个面可以细分为三组，每组有两个相对的面。这三组面分别称为前后面、左右面和上下面，它们具有以下特点：

1. 前后面：它们位于长方体的前后两侧，面积相等，形状相同。它们的边长分别对应长方体的长和宽。

2. 左右面：它们位于长方体的左右两侧，面积相等，形状相同。它们的边长也分别对应长方体的长和宽。

3. 上下面：它们位于长方体的顶部和底部，面积相等，形状相同。它们的边长分别对应长方体的长和高（或者宽和高，具体取决于长方体的摆放方向）。

三、长方体的棱

长方体的棱是连接各个面的顶点的线段。长方体有十二条棱，每条棱的长度都相等或者属于长方体的长、宽、高中的一种。长方体的棱可以细分为三组，每组有四条棱，分别平行且等长：

1. 长度棱：连接前后面顶点的棱，有四条，它们的长度等于长方体的长。

2. 宽度棱：连接左右面顶点的棱，有四条，它们的长度等于长方体的宽。

3. 高度棱：连接上下面顶点的棱，有四条，它们的长度等于长方体的高。

长方体的棱不仅是其结构的组成部分，还是计算其表面积和体积的重要参数。通过测量长方体的棱长，我们可以方便地计算出其表面积和体积。

四、长方体的顶点

长方体的顶点是其各个面的顶点的交点。长方体有八个顶点，每个顶点都是三条棱的交点。这些顶点不仅是长方体结构的重要组成部分，还是确定其位置和形状的关键点。通过连接这些顶点，我们可以构建出长方体的骨架，从而直观地理解其形状和结构。

五、长方体的对称性

长方体是一种高度对称的几何体。它具有以下对称性特征：

1. 中心对称性：长方体的中心是各顶点到该点距离相等的唯一点。以长方体的中心为中心点，任意顶点关于中心点的对称点都在长方体的表面上。

2. 旋转对称性：长方体绕其长、宽、高中的任意一条棱旋转180度后，其形状和位置不变。这种旋转对称性使得长方体在视觉上更加美观和协调。

3. 镜像对称性：长方体关于其任意一条棱的中垂面（即过该棱中点且与该棱垂直的平面）都是镜像对称的。这种对称性使得长方体的形状更加规整和统一。

六、长方体的表面积和体积

长方体的表面积和体积是其重要的几何量，具有广泛的应用价值。

1. 表面积：长方体的表面积是指其所有面的面积之和。根据长方体的特征，我们可以计算出其表面积为：

S = 2lw + 2lh + 2wh

其中，l、w、h分别为长方体的长、宽、高。这个公式可以帮助我们方便地计算出长方体的表面积，用于建筑、家具等领域的计算和规划。

2. 体积：长方体的体积是指其内部所占据的空间大小。根据长方体的特征，我们可以计算出其体积为：

V = lwh

其中，l、w、h分别为长方体的长、宽、高。这个公式是计算长方体体积的基本公式，广泛应用于各种实际问题的求解中。

七、长方体的实际应用

长方体因其独特的形状和性质，在建筑、家具、包装等多个领域有着广泛的应用。

1. 建筑领域：在建筑领域中，长方体是一种常见的几何形状。建筑物的墙体、柱子等结构往往采用长方体形状进行设计，以确保其稳定性和美观性。此外，长方体形状的房间也便于布局和使用，符合人们的居住和办公需求。

2. 家具领域：在家具领域中，长方体形状的家具也非常常见。例如，桌子、椅子、柜子等家具往往采用长方体形状进行设计，以提供足够的储物空间和支撑面积。长方体形状的家具不仅具有实用功能，还具有简洁美观的外观，符合现代家居的审美需求。

3. 包装领域：在包装领域中