高中扇形弧长与面积计算公式详解

在学习高中数学的过程中，扇形的相关知识是一个重要的章节。扇形作为圆的一部分，在几何学中有着广泛的应用。特别是在解决实际问题时，我们经常需要计算扇形的弧长和面积。那么，高中扇形的弧长和面积公式是什么呢？接下来，我们就来详细探讨一下。

首先，我们要明确扇形的基本概念。扇形是指圆上两条半径与它们之间的圆弧所围成的图形。如果我们把圆的周长看作是360度，那么扇形的弧长就是圆周长的一部分，具体占比取决于扇形的圆心角。扇形的面积则是整个圆面积的一部分，占比同样取决于圆心角。

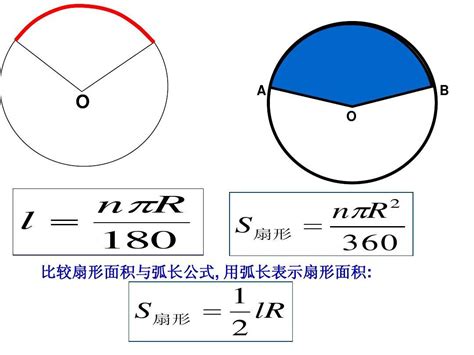
接下来，我们来看扇形的弧长公式。弧长公式的基本形式是：弧长 = 圆心角 × π × 半径 ÷ 180。这里，圆心角用度数表示，π是圆周率，约等于3.14159，半径则是扇形所在圆的半径。通过这个公式，我们可以很方便地计算出扇形的弧长。

例如，我们有一个半径为5厘米的圆，扇形圆心角为60度。那么，扇形的弧长就是：60 × π × 5 ÷ 180 = 5π/3厘米。这个公式在解题过程中非常实用，可以大大提高我们的计算效率。

再来看扇形的面积公式。扇形面积公式的基本形式是：面积 = 圆心角 × π × 半径² ÷ 360。这个公式与弧长公式类似，只不过在计算面积时，我们需要用到半径的平方。同样，圆心角用度数表示，π是圆周率。通过这个公式，我们可以轻松地计算出扇形的面积。

以刚才的例子为例，如果扇形的圆心角为60度，半径为5厘米，那么扇形的面积就是：60 × π × 5² ÷ 360 = 25π/6平方厘米。这个公式同样在解题过程中发挥着重要的作用。

值得注意的是，扇形面积公式还有一种等价形式，即面积 = 1/2 × 弧长 × 半径。这个公式在知道弧长和半径的情况下，可以更快地计算出扇形的面积。同样以上面的例子为例，如果扇形的弧长为5π/3厘米，半径为5厘米，那么扇形的面积就是：1/2 × 5π/3 × 5 = 25π/6平方厘米。这个结果与通过圆心角和半径计算出的面积结果是一致的。

在实际应用中，我们可能会遇到一些需要综合运用扇形弧长和面积公式的问题。例如，已知扇形的面积和圆心角，求扇形的半径或弧长；或者已知扇形的弧长和半径，求扇形的面积和圆心角等。解决这些问题时，我们需要灵活运用弧长和面积公式，进行代数运算和方程求解。

此外，扇形在几何学和实际问题中还有很多应用。例如，在建筑设计中，我们可能需要计算扇形窗户的面积；在制造业中，我们可能需要计算扇形零件的尺寸；在航空航天领域，我们可能需要计算扇形机翼的弧长等。这些应用都需要我们熟练掌握扇形弧长和面积公式的计算方法。

当然，在学习扇形弧长和面积公式的过程中，我们还需要注意一些容易出错的地方。例如，在计算弧长时，要确保圆心角用度数表示；在计算面积时，要注意半径的单位要统一；在综合运用弧长和面积公式时，要仔细审题，明确已知条件和求解目标等。

此外，还有一些常见的题型和解题技巧也值得我们掌握。例如，在求解扇形面积时，如果题目给出的是扇形的周长（包括两条半径和一条弧长），我们可以先通过周长公式求出扇形的弧长，然后再利用面积公式求解。又例如，在求解扇形圆心角时，我们可以通过弧长和半径求出扇形的弧度数，然后再将弧度数转换为度数。

总之，高中扇形的弧长和面积公式是几何学中的重要内容。通过熟练掌握这些公式及其应用方法，我们可以更好地解决与扇形相关的实际问题。同时，这些公式和方法也是我们进一步学习高等数学和其他学科知识的基础。

在学习过程中，我们还要注重培养自己的几何直觉和空间想象力。通过多观察、多思考、多练习，我们可以更好地理解扇形的性质和相关公式。此外，我们还可以借助一些几何图形软件和工具来帮助我们进行可视化学习和实践操作。这些软件和工具可以让我们更加直观地看到扇形的形状和变化过程，从而加深我们对相关公式的理解和记忆。

最后，我们要强调的是，学习扇形弧长和面积公式不仅仅是为了应对考试和解题。更重要的是，通过学习和应用这些公式，我们可以培养自己的逻辑思维能力和解决问题的能力。这些能力对于我们未来的学习和工作都是非常重要的。

因此，在学习高中扇形弧长和面积公式的过程中，我们要保持积极的态度和耐心的心态。通过不断努力和实践，我们一定能够掌握这些公式及其应用方法，并在实际问题中发挥出它们的价值。同时，我们也要注重培养自己的几何直觉和空间想象力，为未来的学习和工作打下坚实的基础。