竖式除法的正确格式是什么

除法竖式是数学运算中常见的一种格式，它能够帮助我们清晰地理解除法的步骤和结果。在数学学习中，除法竖式特别适用于解决那些较为复杂的除法问题，尤其是当被除数较大或者除数不是整数时。通过竖式，我们可以一步步地进行运算，直到得出最终的结果。

首先，我们需要明确除法竖式的基本结构。竖式通常分为三层：被除数层、除数层和商层。被除数是我们需要被分解的那个数，它通常位于竖式的最上方。除数则是用来去除被除数的那个数，它位于被除数的左下方。商则是除法运算的结果，它位于竖式的最下方，通过一系列的步骤来逐步确定。

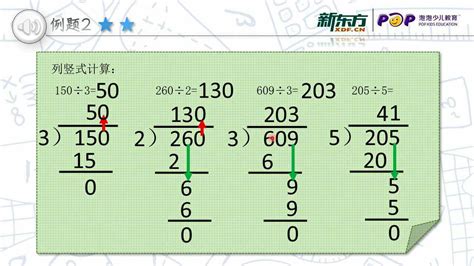
在进行除法竖式运算时，我们首先将被除数的最高位（或最高几位）写下来，如果这一位（或几位）小于除数，那么我们就需要将被除数的下一位（或几位）也写下来，直到组成的数大于或等于除数为止。然后，我们将这个数除以除数，得出的结果就是商的第一位。接下来，我们将这个商与被除数的下一位（或几位）组合起来，形成一个新的数，再除以除数，得到商的下一位。这个过程一直重复，直到被除数被完全除尽，或者只剩下余数为止。

例如，我们来解决一个简单的除法问题：42除以3。首先，我们在竖式中被除数的位置写下42，除数的位置写下3。然后，我们将被除数的最高位4写下来，由于4大于3，我们可以直接进行除法运算。4除以3得出的商是1，所以我们将1写在竖式的商层。然后，我们将商1与被除数的下一位2组合起来，形成新的数12。12再除以3得出的商是4，所以我们继续在商层写下4。此时，被除数已经被完全除尽，没有余数，所以我们的答案是14。

再来看一个稍微复杂一点的例子：100除以7。首先，我们在竖式中被除数的位置写下100，除数的位置写下7。然后，我们将被除数的最高两位10写下来，由于10小于7，我们需要将被除数的下一位也写下来，形成新的数100（实际上在这个例子中，我们一开始就写下了整个被除数，因为被除数只有三位，且最高两位小于除数）。接着，我们用100除以7，得出的商是14（因为7乘以14等于98，而98小于100但最接近100），所以我们将14的前一位1写在竖式的商层，表示商的十位数。然后，我们将100减去98（7乘以14的结果），得到余数2。接下来，我们将这个余数2与被除数的下一位（实际上在这个例子中已经没有下一位了，因为被除数已经被用完）组合起来，形成新的数20（这里实际上是将余数2看作20的十位数，个位数为0）。但是注意，由于被除数已经用完，我们不能真的再加上一个0，这里的20只是用来表示余数和下一个可能的被除数位（如果有的话）的组合。然而，在这个例子中，我们并不需要真的加上一个0，因为2已经小于除数7了，所以我们直接用2除以7。由于2小于7，所以商的这一位是0。然后，我们将这个余数2保留下来，表示除法运算的结果是一个商14余2的数。

通过这两个例子，我们可以看到除法竖式在解决除法问题时的清晰性和实用性。它不仅能够让我们一步步地进行运算，避免出错，还能够让我们更好地理解除法的本质和过程。

除法竖式还常用于处理那些涉及到小数或分数的除法问题。当被除数或除数是小数时，我们可以先将它们转化为整数（通过乘以适当的10的幂次），然后使用整数除法竖式进行运算。最后，再将结果转化为小数（通过除以适当的10的幂次）。同样地，当被除数或除数是分数时，我们可以先将它们转化为具有相同分母或可通分的分数的形式，然后使用分数除法竖式进行运算（分数除法通常转化为乘法进行运算）。

此外，除法竖式还可以用于解决那些涉及到长除法的问题，如多项式除法。在长除法中，我们将一个多项式除以另一个多项式，得到的商是一个多项式，余数也是一个多项式（如果有的话）。通过使用竖式，我们可以清晰地看到每一步的运算过程，从而更容易地得出正确的结果。

总之，除法竖式是一种非常有用的数学工具，它能够帮助我们更好地理解和解决除法问题。无论是在处理整数、小数还是分数的除法问题时，还是在解决长除法问题时，除法竖式都能够提供清晰、准确的运算过程和结果。因此，在学习数学的过程中，我们应该熟练掌握除法竖式的使用方法和技巧，以便更好地应对各种除法问题。