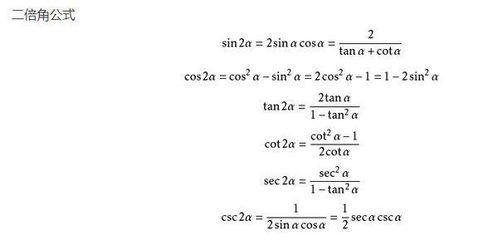幂的运算法则是什么?
幂的运算法则,是数学领域中一项基础而强大的工具,它如同一把钥匙,解锁了代数世界的诸多奥秘。在数学的浩瀚星空中,幂的运算如同璀璨星辰,引领我们探索数与式之间的规律与联系。本文将从幂的定义出发,逐步深入,从代数、几何、应用及思维拓展等多个维度,揭示幂的运算法则的魅力与实用性。

幂的定义:数的自我迭代
幂,简而言之,是一个数自我相乘的结果。当我们说a的n次幂,记作a^n,意味着将a这个数自乘n次。例如,2^3表示2乘以自己两次,即2×2×2=8。幂的概念不仅限于正整数指数,它还拓展到了零、负整数、分数乃至复数等更广泛的领域,形成了完整的幂运算体系。

代数维度:法则的推导与应用
幂的运算法则是代数学习的核心内容之一,它们包括同底数幂的乘法、除法、幂的乘方以及积的乘方等。

同底数幂的乘法:当底数相同时,指数相加。即a^m * a^n = a^(m+n)。这一法则揭示了幂运算中的“加法”性质,是化简复杂表达式的关键。
同底数幂的除法:当底数相同时,指数相减。即a^m ÷ a^n = a^(m-n)(a ≠ 0,m和n为正整数,且m > n时,结果为正;m < n时,结果为a^(m-n)的倒数)。这一法则对应了幂运算中的“减法”性质,为求解幂的比值问题提供了便捷途径。
幂的乘方:幂的指数相乘。即(a^m)^n = a^(m×n)。这一法则展示了幂运算的“乘法”性质,它允许我们将复杂的幂运算转化为更简单的形式。
积的乘方:(ab)^n = a^n * b^n。这一法则揭示了幂运算在乘法下的分配律,为处理含有多个因子的幂运算提供了有效方法。
几何维度:直观理解幂的增长
幂运算的几何意义同样深远。以二维平面为例,正方形的面积与其边长的平方成正比,即面积A = s^2,这里的s为边长。当我们增加边长时,面积的增长速度是边长的平方倍,这直观展示了幂运算(特别是二次幂)的快速增长特性。同理,在三维空间中,正方体的体积与其边长的三次幂成正比,V = s^3,进一步体现了幂运算的几何意义及其增长速度的急剧变化。
应用维度:现实世界的数学模型
幂的运算法则在现实生活中的应用无处不在,从物理学中的自由落体运动、牛顿冷却定律,到经济学中的复利计算、人口增长模型,再到计算机科学中的算法复杂度分析,幂运算都是不可或缺的数学工具。
复利计算:在金融领域,复利计算依赖于幂运算。假设本金为P,年利率为r,存款年数为t,则t年后的本息总和F = P(1 + r)^t,这里的指数t表示时间,体现了资金随时间呈指数级增长的特点。
物理学中的自由落体:在忽略空气阻力的情况下,物体从静止自由下落的高度h与时间t的关系为h = 1/2gt^2,其中g为重力加速度。这里的二次幂t^2直观展示了物体下落高度随时间的平方增长。
算法复杂度:在计算机科学中,算法的时间复杂度和空间复杂度常用幂函数来描述。例如,一个线性搜索算法的时间复杂度为O(n),而一个排序算法如快速排序的平均时间复杂度为O(n log n),这里的n表示问题的规模,幂运算帮助我们判断算法的效率。
思维拓展:幂运算的哲学思考
幂的运算法则不仅限于数学计算,它还蕴含着深刻的哲学思考。幂运算展示了数量的累积效应,即小的变化在重复多次后可能引发巨大的结果。这正如“滴水穿石,非一日之功”,强调了持续努力的重要性。同时,幂运算中的指数增长和衰减也提醒我们,在面对资源分配、疾病传播等问题时,初期的小变化可能对未来产生深远的影响,强调了预防和早期干预的价值。
此外,幂运算还体现了数学中的抽象与统一之美。无论是物理、经济还是计算机科学,幂运算都能以简洁的形式描述复杂的现象,这种跨领域的适用性展示了数学作为人类思维工具的强大力量。
结语
幂的运算法则,作为数学殿堂中的一块基石,以其简洁而强大的形式,连接了代数、几何、应用等多个领域,展现了数学之美与实用性的完美结合。通过深入理解幂的运算法则,
- 上一篇: 细叶榕怎么养殖?注意事项有哪些?
- 下一篇: 如何在网易云音乐中设置一起听歌功能?
-
 幂运算常用的8个公式分别是什么?资讯攻略11-11
幂运算常用的8个公式分别是什么?资讯攻略11-11 -
 市场营销学中,FABE法则具体代表什么?资讯攻略10-25
市场营销学中,FABE法则具体代表什么?资讯攻略10-25 -
 二次根式乘除法则是什么?资讯攻略01-10
二次根式乘除法则是什么?资讯攻略01-10 -
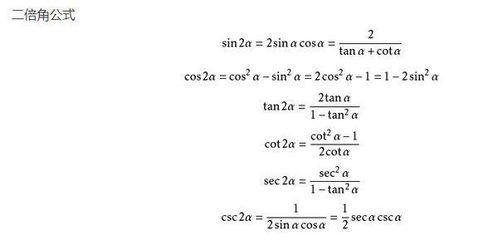 精通常见三角函数积分:公式推导与全面总结资讯攻略11-18
精通常见三角函数积分:公式推导与全面总结资讯攻略11-18 -
 C语言中表示不等于的符号是什么资讯攻略11-18
C语言中表示不等于的符号是什么资讯攻略11-18 -
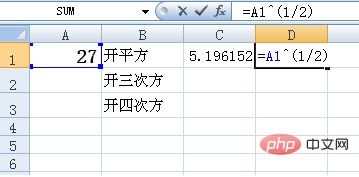 三次方公式具体是什么?资讯攻略11-09
三次方公式具体是什么?资讯攻略11-09