揭秘!正方形周长的神奇计算公式,一看就会
正方形,这一几何形状自古以来便在人类文明中扮演着重要角色。从建筑设计到艺术创作,从日常生活用品到复杂的科学仪器,正方形的身影无处不在。它的四个等边和四个直角赋予了它独特的魅力和实用性。今天,我们就来深入探讨一个关于正方形的基本属性——周长,以及正方形的周长公式是如何得出的。

首先,让我们明确正方形的定义。正方形是一种四边形,它的四条边都相等,且四个角都是直角。这个定义简洁明了,却蕴含了正方形所有的基本性质。由于正方形的四条边都相等,我们可以设其边长为a。
接下来,我们引入周长的概念。周长,简单来说,就是一个平面图形边界的总长度。对于正方形来说,周长就是它四条边的长度之和。由于正方形的四条边都相等,因此,我们只需要将边长a乘以4,就可以得到正方形的周长。

这个简单的乘法运算,就是正方形的周长公式:P = 4a。其中,P代表周长,a代表边长。这个公式不仅简洁明了,而且非常实用。无论是在日常生活中计算正方形的周长,还是在更复杂的几何问题中运用这个公式,它都能为我们提供准确的答案。
然而,公式虽然简单,但其背后的数学原理却值得我们深入探究。正方形的周长公式,实际上是基于正方形的基本性质——四条边相等这一事实得出的。这一性质不仅决定了正方形的形状和大小,也决定了它的周长计算方式。当我们说一个正方形的周长是某个值时,我们实际上是在说它的四条边的总长度是这个值。
此外,正方形的周长公式还与几何学的其他概念紧密相连。例如,当我们谈论正方形的面积时,我们通常会提到另一个公式:S = a²。这个公式表示正方形的面积是边长的平方。虽然周长和面积是两个不同的概念,但它们都依赖于正方形的边长a。这种联系不仅体现了几何学内部各概念之间的紧密联系,也为我们解决实际问题提供了更多的思路和方法。
在实际应用中,正方形的周长公式有着广泛的应用。在建筑设计中,工程师们常常需要计算正方形的周长来确定建筑材料的用量。在艺术创作中,艺术家们可以利用正方形的周长来设计作品的尺寸和布局。在日常生活中,我们也可以用正方形的周长公式来计算房间的周长、桌子的周长等。这些应用不仅展示了正方形周长公式的实用性,也体现了数学与生活的紧密联系。
当然,正方形的周长公式并不仅仅局限于二维平面内的计算。在三维空间中,我们也可以将正方形的周长公式应用于立方体的棱长计算。立方体是一个由六个正方形面组成的立体图形,它的每个面都是一个正方形。因此,我们可以利用正方形的周长公式来计算立方体每条棱的长度(即正方形的边长)。这种应用不仅拓展了正方形周长公式的应用范围,也为我们解决三维空间中的几何问题提供了新的思路和方法。
除了在建筑、艺术和日常生活中的应用外,正方形的周长公式还在其他学科领域发挥着重要作用。在物理学中,正方形的周长公式可以用于计算电荷在正方形导体中的分布;在化学中,它可以用于估算分子或原子在正方形排列中的距离;在计算机科学中,它可以用于设计算法来优化正方形图形的渲染效率。这些应用不仅展示了正方形周长公式的广泛适用性,也体现了数学作为一门基础学科的重要性。
此外,正方形的周长公式还与数学中的其他概念有着紧密的联系。例如,它可以与比例、分数、小数等数学概念相结合,用于解决更复杂的数学问题。同时,它也可以作为学习更高级数学概念的起点和基础。在学习代数、几何、微积分等数学分支时,我们经常会遇到与正方形周长相关的题目和问题。通过解决这些问题,我们不仅可以巩固对正方形周长公式的理解,还可以逐步掌握更高级的数学知识和方法。
总之,正方形的周长公式是一个简单而实用的数学工具。它不仅能够帮助我们快速准确地计算正方形的周长,还能够为我们解决更复杂的几何问题和实际问题提供思路和方法。同时,它还与数学中的其他概念紧密相连,为我们学习更高级的数学知识和方法奠定了基础。因此,无论是在学习、工作还是生活中,掌握正方形的周长公式都是非常重要的。
最后,我想强调的是,数学不仅仅是一门学科,更是一种思维方式和方法论。通过学习和运用数学知识,我们可以更好地理解世界、解决问题和创新创造。而正方形的周长公式作为数学中的一个基本概念和工具,正是我们培养数学思维和方法的起点之一。因此,让我们珍视这个简单的公式,用心去感受它背后的数学魅力和智慧吧!
- 上一篇: 如何轻松开设港股账户?
- 下一篇: 问答解锁:hardest2第11-18关全攻略,图文详解助你通关!
-
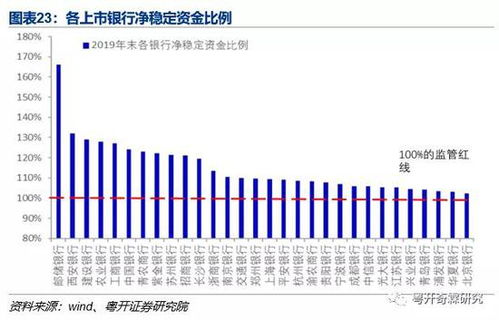 存贷比计算公式详解,一看就懂!资讯攻略10-31
存贷比计算公式详解,一看就懂!资讯攻略10-31 -
 揭秘长方体周长的神奇计算公式!资讯攻略11-19
揭秘长方体周长的神奇计算公式!资讯攻略11-19 -
 轻松学会!千纸鹤折纸步骤图解,一看就会的简易教程资讯攻略01-24
轻松学会!千纸鹤折纸步骤图解,一看就会的简易教程资讯攻略01-24 -
 如何手工折叠简单的金元宝?一看就会的折法教程资讯攻略02-01
如何手工折叠简单的金元宝?一看就会的折法教程资讯攻略02-01 -
 正方形周长计算公式详解资讯攻略10-31
正方形周长计算公式详解资讯攻略10-31 -
 揭秘!如何正确书写大写数字,一看就会的实用技巧资讯攻略10-25
揭秘!如何正确书写大写数字,一看就会的实用技巧资讯攻略10-25











