解锁数据奥秘:全面汇总资料分析必备公式
在商业、科学、教育、社会学等众多领域中,资料分析扮演着至关重要的角色。它是通过一系列方法和工具,从原始数据中提取有用信息,以支持决策制定、理论验证或问题解决的过程。资料分析公式汇总,作为这一过程的基石,提供了一系列经过验证的数学和统计工具,帮助分析者高效地处理和理解数据。本文将从基础统计量、概率分布、假设检验、回归分析、时间序列分析以及数据挖掘等多个维度,介绍资料分析中常用的公式和概念。
基础统计量
基础统计量是资料分析的起点,它们提供了数据集的基本描述,包括集中趋势、离散程度和分布形态等。
1. 均值(Mean):表示数据集的平均水平,计算公式为所有数值之和除以数值的数量。
\[
\text{Mean} = \frac{\sum_{i=1}^{n} x_i}{n}
\]
2. 中位数(Median):将数据从小到大排序后位于,中间的数值。如果数据量为奇数,中位数是中间那个数;如果为偶数,则是中间两个数的平均值。
3. 众数(Mode):数据集中出现次数最多的数值。
4. 方差(Variance):衡量数据离散程度的指标,计算每个数值与均值之差的平方的平均值。
\[
\text{Variance} = \frac{\sum_{i=1}^{n} (x_i - \text{Mean})^2}{n}
\]
5. 标准差(Standard Deviation):方差的平方根,具有与数据相同单位的度量,更直观地表示数据的离散程度。
\[
\text{Standard Deviation} = \sqrt{\text{Variance}}
\]
概率分布
概率分布描述了随机变量可能取值的概率规律,是统计学和概率论的核心内容。
1. 正态分布(Normal Distribution):又称高斯分布,是最常见的连续概率分布,由均值和标准差两个参数决定。其概率密度函数为:
\[
f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}
\]
其中,\(\mu\)为均值,\(\sigma\)为标准差。
2. 二项分布(Binomial Distribution):用于描述在固定次数的独立试验中,成功次数的概率分布。概率质量函数为:
\[
P(X=k) = C(n, k) p^k (1-p)^{(n-k)}
\]
其中,\(n\)为试验次数,\(k\)为成功次数,\(p\)为单次成功的概率。
3. 泊松分布(Poisson Distribution):用于描述在固定时间或空间内某事件发生的次数的概率分布,适用于稀有事件且事件间相互独立的情况。概率质量函数为:
\[
P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}
\]
其中,\(\lambda\)为事件发生的平均速率。
假设检验
假设检验是一种统计方法,用于判断样本数据是否支持关于总体参数的某个假设。
1. Z检验:用于大样本情况下,检验样本均值与已知或假设的总体均值是否存在显著差异。统计量为:
\[
Z = \frac{\bar{X} - \mu_0}{\frac{\sigma}{\sqrt{n}}}
\]
其中,\(\bar{X}\)为样本均值,\(\mu_0\)为假设的总体均值,\(\sigma\)为总体标准差,\(n\)为样本大小。
2. t检验:用于小样本情况下,或当总体标准差未知时,检验样本均值与假设的总体均值是否存在显著差异。统计量为:
\[
t = \frac{\bar{X} - \mu_0}{S/\sqrt{n}}
\]
其中,\(S\)为样本标准差。
回归分析
回归分析是一种预测性建模技术,它研究一个或多个自变量(预测变量)与因变量(响应变量)之间的关系。
1. 简单线性回归:模型形式为\(Y = \beta_0 + \beta_1X + \epsilon\),其中\(\beta_0\)为截距,\(\beta_1\)为斜率,\(\epsilon\)为误差项。回归系数的估计通常使用最小二乘法。
2. 多元线性回归:当存在多个自变量时,模型形式为\(Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_kX_k + \epsilon
- 上一篇: 揭秘:天津李四的真实身份是什么?
- 下一篇: 轻松学会!蝴蝶结的简单折纸教程
-
 全面解锁!24个必备二重积分公式汇总资讯攻略01-19
全面解锁!24个必备二重积分公式汇总资讯攻略01-19 -
 Excel常用公式与高效计算方法指南资讯攻略11-19
Excel常用公式与高效计算方法指南资讯攻略11-19 -
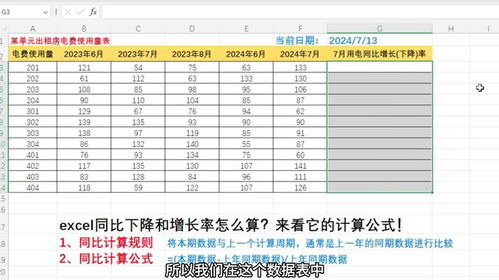 同比增幅的奥秘:掌握这个计算公式,让数据对比一目了然资讯攻略11-04
同比增幅的奥秘:掌握这个计算公式,让数据对比一目了然资讯攻略11-04 -
 掌握进化树分析方法,解锁生命奥秘资讯攻略02-08
掌握进化树分析方法,解锁生命奥秘资讯攻略02-08 -
 Excel中如何进行数值相减的函数公式是什么?资讯攻略12-05
Excel中如何进行数值相减的函数公式是什么?资讯攻略12-05 -
 Excel高手必备:深入解析COUNTA统计函数资讯攻略11-30
Excel高手必备:深入解析COUNTA统计函数资讯攻略11-30












