如何判断函数的奇偶性才是最好的方法?
在数学中,函数的奇偶性是一个重要而基础的概念。它不仅帮助我们理解函数的性质,还能简化很多计算和分析过程。本文将详细介绍判断函数奇偶性的几种方法,并探讨其中的“最好”方法。通过理解这些方法的适用条件和优缺点,读者可以更加全面地掌握这一知识点。
一、奇偶性的定义
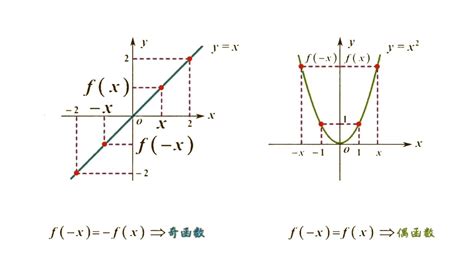
首先,我们需要明确函数奇偶性的定义。设函数f(x)的定义域为D,如果对于D内的任意x,都有f(-x)=-f(x),则称f(x)为奇函数;如果对于D内的任意x,都有f(-x)=f(x),则称f(x)为偶函数。如果函数既不满足奇函数的定义,也不满足偶函数的定义,则称该函数为非奇非偶函数。
二、常见的判断方法
1. 代数法
代数法是最直观的判断方法。对于给定的函数f(x),我们直接计算f(-x),然后比较f(-x)与f(x)的关系。
如果f(-x)=-f(x),则f(x)是奇函数。
如果f(-x)=f(x),则f(x)是偶函数。
例1:判断函数f(x)=x^3-x的奇偶性。
计算f(-x):f(-x)=(-x)^3-(-x)=-x^3+x=-(x^3-x)=-f(x)。
因此,f(x)=x^3-x是奇函数。
例2:判断函数f(x)=x^2+1的奇偶性。
计算f(-x):f(-x)=(-x)^2+1=x^2+1=f(x)。
因此,f(x)=x^2+1是偶函数。
2. 图像法
图像法是通过观察函数的图像来判断其奇偶性。
如果函数图像关于原点对称,则函数是奇函数。
如果函数图像关于y轴对称,则函数是偶函数。
这种方法直观易懂,但前提是能够准确地画出函数的图像。对于一些复杂函数,图像可能难以绘制或观察。
例3:判断函数f(x)=sin(x)的奇偶性。
观察sin(x)的图像,我们发现它关于原点对称。因此,f(x)=sin(x)是奇函数。
例4:判断函数f(x)=cos(x)的奇偶性。
观察cos(x)的图像,我们发现它关于y轴对称。因此,f(x)=cos(x)是偶函数。
3. 定义域法
定义域法是通过分析函数的定义域来判断其奇偶性。
如果函数的定义域不关于原点对称,则函数既不是奇函数也不是偶函数。
如果函数的定义域关于原点对称,但f(-x)与f(x)没有确定的关系,则函数也是非奇非偶函数。
这种方法快速有效,但只能排除一些显然非奇非偶的情况,不能给出函数是奇函数还是偶函数的明确答案。
例5:判断函数f(x)=1/x的奇偶性。
函数f(x)=1/x的定义域为{x|x≠0},这个定义域关于原点对称。计算f(-x):f(-x)=-1/x=-f(x)。因此,f(x)=1/x是奇函数。
例6:判断函数f(x)=√x的奇偶性。
函数f(x)=√x的定义域为[0,+∞),这个定义域不关于原点对称。因此,f(x)=√x是非奇非偶函数。
4. 性质法
性质法是利用函数的已知性质来判断其奇偶性。例如,如果知道函数是周期函数,可以结合周期性和奇偶性的关系来判断。这种方法适用于一些特殊类型的函数,如三角函数、指数函数等。
例7:判断函数f(x)=e^x的奇偶性。
函数f(x)=e^x是指数函数,其图像既不关于原点对称也不关于y轴对称。计算f(-x):f(-x)=e^(-x)=1/e^x≠e^x且≠-e^x。因此,f(x)=e^x是非奇非偶函数。
例8:判断函数f(x)=tan(x)的奇偶性。
函数f(x)=tan(x)是正切函数,其
- 上一篇: 揭秘医学术语“NOS”:它究竟代表什么?
- 下一篇: 如何高效练习篮球拉杆动作
-
 揭秘奇偶性的判断秘籍资讯攻略11-03
揭秘奇偶性的判断秘籍资讯攻略11-03 -
 奇偶函数相加,结果竟是?奇+奇、偶+偶、奇+偶分别得到什么函数?资讯攻略01-29
奇偶函数相加,结果竟是?奇+奇、偶+偶、奇+偶分别得到什么函数?资讯攻略01-29 -
 在Excel中如何输入函数来判断数值是否大于等于特定值?资讯攻略10-25
在Excel中如何输入函数来判断数值是否大于等于特定值?资讯攻略10-25 -
 如何在Excel中使用RANK函数?资讯攻略11-11
如何在Excel中使用RANK函数?资讯攻略11-11 -
 《DNF深度解析:揭秘佣兵军团中,哪个职业才是你的最强战魂?》资讯攻略10-20
《DNF深度解析:揭秘佣兵军团中,哪个职业才是你的最强战魂?》资讯攻略10-20 -
 Excel中COUNTIF函数的使用方法资讯攻略11-26
Excel中COUNTIF函数的使用方法资讯攻略11-26











