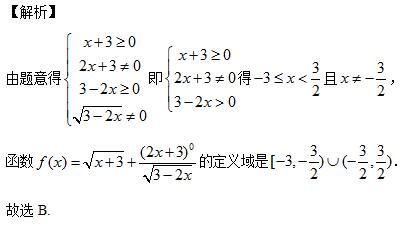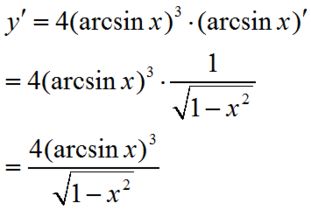log函数的导数如何求解?
在数学的广阔领域中,对数函数及其导数扮演着举足轻重的角色。它们不仅在理论研究上占据一席之地,更在实际应用中发挥着重要作用。本文旨在深入探讨log函数的求导公式,帮助读者全面理解这一核心概念。

首先,我们需要明确对数函数的基本概念。对数函数是以幂(真数)为自变量、以指数为因子的函数。常见的对数函数有自然对数函数(以e为底)和常用对数函数(以10为底)。对数函数的形式通常为y=log_a(x),其中a为底数,x为真数。对于自然对数函数,底数e(约等于2.71828)是一个特殊的常数,它在数学和物理中具有许多独特的性质。

接下来,我们进入本文的主题——log函数的求导公式。对于自然对数函数ln(x),其导数相对简单,为1/x。这一结果在数学和物理中都有广泛的应用,特别是在处理与指数函数、对数函数相关的问题时。自然对数函数的导数公式可以通过链式法则和对数的定义来推导。

链式法则是一种计算复合函数导数的方法。对于复合函数y=f(g(x)),其导数y'可以通过f'(g(x))和g'(x)的乘积来求得。应用到自然对数函数上,我们可以将ln(x)视为f(u)和g(x)的复合函数,其中f(u)=ln(u),g(x)=x。根据链式法则,我们有d/dx(ln(x))=f'(g(x))*g'(x)。由于f'(u)=1/u(对数函数的导数性质),g'(x)=1(线性函数的导数),所以d/dx(ln(x))=1/x。

对于常用对数函数log(x)(以10为底),其导数稍微复杂一些,为1/(x*ln(10))。这个公式同样可以通过链式法则来推导。我们将log(x)视为f(u)和g(x)的复合函数,其中f(u)=log(u)(以10为底的对数函数),g(x)=x。根据链式法则,我们有d/dx(log(x))=f'(g(x))*g'(x)。由于f'(u)=1/(u*ln(10))(常用对数函数的导数性质),g'(x)=1(线性函数的导数),所以d/dx(log(x))=1/(x*ln(10))。
除了自然对数函数和常用对数函数外,我们还经常遇到以其他数为底的对数函数log_a(x)。对于这类函数,其导数公式为1/(x*ln(a)),其中a为底数,x为真数。这个公式可以通过换底公式和链式法则来推导。换底公式允许我们将以a为底的对数函数转化为自然对数函数的形式,即log_a(x)=ln(x)/ln(a)。然后,我们利用自然对数函数的导数结果和链式法则,可以得到log_a(x)的导数为1/(x*ln(a))。
在理解和应用log函数的求导公式时,我们需要注意以下几点:
首先,导数是函数在某一点的变化率,它描述了函数图像在该点的切线斜率。因此,理解导数的定义和性质对于掌握log函数的求导公式至关重要。
其次,链式法则和换底公式在推导log函数的导数时起着重要作用。链式法则允许我们将复合函数的导数分解为各个部分函数的导数的乘积,而换底公式则允许我们将以任意数为底的对数函数转化为自然对数函数的形式。
此外,我们还需要注意对数函数的定义域。对于自然对数函数ln(x),其定义域为x>0;对于常用对数函数log(x)(以10为底),其定义域同样为x>0;对于以a为底的对数函数log_a(x),其定义域为x>0且a>0且a≠1。在求导时,我们需要确保自变量x在函数的定义域内。
最后,让我们通过一些例子来加深对log函数求导公式的理解。
例1:求函数y=ln(x^2+1)的导数。
解:这是一个复合函数,我们可以将其视为f(u)和g(x)的复合函数,其中f(u)=ln(u),g(x)=x^2+1。根据链式法则,我们有y'=f'(g(x))*g'(x)。由于f'(u)=1/u,g'(x)=2x,所以y'=1/(x^2+1)*2x=2x/(x^2+1)。
例2:求函数y=log_2(x^3-1)
- 上一篇: 女娲的拼音怎么拼
- 下一篇: 掌握中国电信停机保号办理秘籍,轻松保留号码无忧!
-
 对数函数的导数详解资讯攻略10-28
对数函数的导数详解资讯攻略10-28 -
 2x的导数求解,一看就懂!资讯攻略11-06
2x的导数求解,一看就懂!资讯攻略11-06 -
 什么是高等数学入门中的曲线拐点?如何求解?资讯攻略11-20
什么是高等数学入门中的曲线拐点?如何求解?资讯攻略11-20 -
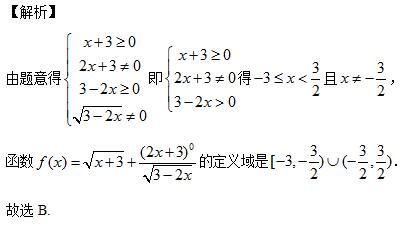 log函数的定义域是什么资讯攻略11-29
log函数的定义域是什么资讯攻略11-29 -
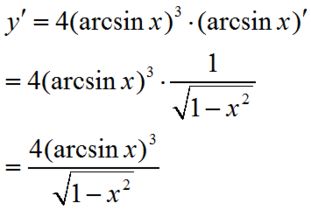 如何推导arctan函数的导数资讯攻略12-07
如何推导arctan函数的导数资讯攻略12-07 -
 掌握函数求导的实用方法资讯攻略10-29
掌握函数求导的实用方法资讯攻略10-29