长方体展开图全解析:到底有多少种变化?
在我们日常生活中,长方体是一个再常见不过的几何体了。无论是书本、盒子还是房间,都可以近似地看作是一个长方体。而当我们想要把这个三维的长方体“拆开”并铺展成一个二维的平面图形时,就会得到长方体的展开图。那么,这个看似简单的操作,到底能有多少种不同的展开方式呢?大神们,咱们一起来探究一下吧!

首先,咱们得明确一下什么是长方体的展开图。简单来说,就是把一个长方体的六个面(上、下、前、后、左、右)按照某种方式剪开,然后铺展在平面上,形成一个连续的、没有重叠的平面图形。这个过程就像是我们拆礼物盒时,把盒子的各个面都拆开,然后平铺开来一样。

现在,我们来想象一下一个最简单的长方体——它的每个面都是正方形,也就是一个正方体。对于正方体来说,由于它的每个面都相等,所以展开图会比较容易想象。但是,即使是正方体,展开图也不是只有一种哦!我们可以试着想象一下,从正方体的一个顶点出发,沿着不同的棱把各个面都剪开,然后铺展开来。通过不同的剪法,我们可以得到不同的展开图。
那么,对于一般的长方体来说,展开图的种类就更多了。因为长方体的每个面都可以有不同的尺寸和形状,所以剪开和铺展的方式也就更加多样化。不过,别担心,我们可以通过一些规律和方法来找出所有可能的展开图。
为了简化问题,我们可以先考虑长方体的一种特殊情况——每个面的尺寸都不同的长方体。这种长方体虽然在实际生活中不太常见,但是对于我们理解展开图的种类却很有帮助。对于这种情况下的长方体,我们可以先确定一个固定的面作为起点(比如上面),然后从这个面出发,沿着不同的棱把其他各个面都剪开。由于每个面的尺寸都不同,所以剪开和铺展的方式就会受到很大的限制。通过逐步尝试和排列组合,我们可以找出所有可能的展开图。
当然,对于一般的长方体来说,由于可能存在尺寸相同的面,所以展开图的种类会更多。比如,如果一个长方体有两个相对的面尺寸相同,那么这两个面在展开图中就可以互换位置。这样一来,就会增加展开图的种类。
那么,到底有多少种不同的长方体展开图呢?这个问题其实没有一个简单的答案,因为它取决于长方体的具体尺寸和形状。不过,我们可以通过一些方法来估算或者找出所有可能的展开图。比如,我们可以利用计算机程序来进行穷举搜索,通过排列组合的方式找出所有可能的展开图。这种方法虽然比较繁琐,但是可以保证找到所有可能的解。
另外,我们还可以利用一些数学知识和规律来简化问题。比如,我们可以先确定一个固定的面作为起点,然后考虑其他各个面与这个面的相对位置关系。通过这种方式,我们可以把问题转化为一个图论问题或者排列组合问题,然后利用相关的数学知识来解决。
不过,值得注意的是,即使我们找到了所有可能的展开图,也不意味着这些展开图都是唯一的或者都有意义的。因为在实际应用中,我们可能需要考虑长方体的具体用途和制造工艺等因素。比如,如果我们想要制作一个长方体形状的包装盒,那么我们就需要确保展开图能够方便地折叠成盒子,并且盒子的各个面都能够完美地贴合在一起。这就需要我们在设计展开图时考虑到一些实际的因素和限制。
此外,长方体展开图的问题还与一些其他的数学问题有着密切的联系。比如,它与图论中的路径问题和排列组合问题有着相似之处;它与几何中的折叠和展开问题也有着紧密的联系。通过研究这些问题,我们可以更深入地理解长方体展开图的本质和规律。
那么,回到我们最初的问题:长方体展开图有多少种?现在我们可以得出结论了:这个问题没有一个固定的答案,它取决于长方体的具体尺寸和形状以及我们的具体需求和限制。不过,通过利用数学知识和规律以及计算机程序等工具,我们可以找出所有可能的展开图,并且从中选择出最适合我们需求的解。
最后,我想说的是:长方体展开图的问题虽然看似简单,但是它背后却隐藏着丰富的数学知识和规律。通过研究这个问题,我们可以更好地理解和应用数学知识,同时也可以培养我们的逻辑思维能力和创造力。所以,如果你对这个问题感兴趣的话,不妨自己动手试一试吧!说不定你会发现一些新的规律和现象哦!
- 上一篇: 完美焦糖布丁的制作秘籍
- 下一篇: 如何快速找回QQ账号密码
-
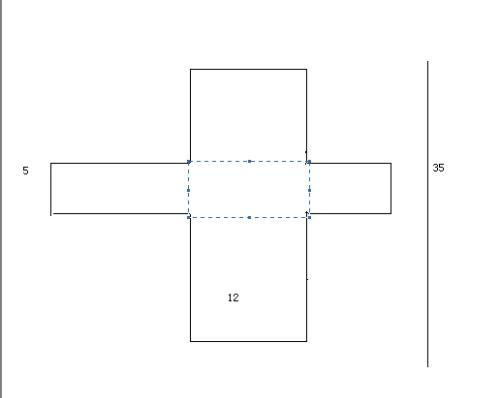 长方体展开图有几种常见的形式?资讯攻略11-17
长方体展开图有几种常见的形式?资讯攻略11-17 -
 如何绘制正方体的11种展开图?资讯攻略11-20
如何绘制正方体的11种展开图?资讯攻略11-20 -
 瑜伽入门必备:莲花坐标准坐姿配图全解析资讯攻略11-02
瑜伽入门必备:莲花坐标准坐姿配图全解析资讯攻略11-02 -
 中美时差到底有多少?资讯攻略02-02
中美时差到底有多少?资讯攻略02-02 -
 揭秘:标准篮球场的面积到底有多大?资讯攻略10-29
揭秘:标准篮球场的面积到底有多大?资讯攻略10-29 -
 揭秘:闰年二月到底有多少天?资讯攻略11-16
揭秘:闰年二月到底有多少天?资讯攻略11-16












