长方体周长怎么计算？

长方体的周长计算，这一看似简单的几何问题，实则蕴含着丰富的数学知识和多维度的思考。长方体，作为三维空间中的基本几何体，其周长（或更准确地说，其表面积）的计算，不仅涉及基本的数学运算，还与我们日常生活中的许多实际应用紧密相连。本文将从长方体的基本概念、周长计算的误区与正确理解、计算公式的推导、实际应用以及数学思维的拓展等多个维度，深入探讨长方体的周长计算。

长方体的基本概念

长方体，又称矩形平行六面体，是三维空间中六个面都是矩形的平行六面体。它的每一对面都相互平行且相等，同时，其相邻的三组对面分别垂直。长方体的三组对边分别称为长、宽、高，通常用a、b、c表示。在三维空间中，长方体以其独特的结构，成为构建复杂几何体的基础。

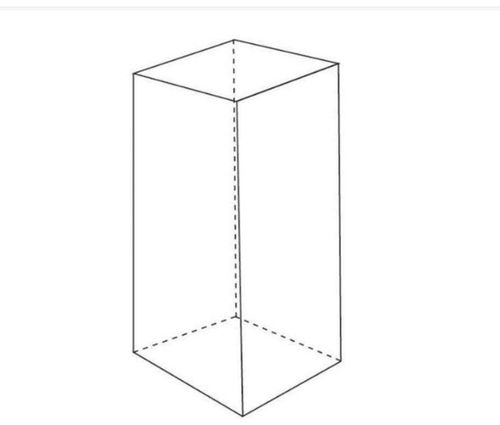
周长计算的误区与正确理解

提到“长方体的周长”，许多人可能会立即联想到二维平面中长方形的周长计算公式（2l+2w）。然而，在三维空间中，长方体的“周长”概念需要被重新定义。实际上，在三维几何中，我们更多地谈论的是长方体的表面积，而非周长。长方体的表面积是指其所有六个面的面积之和，而周长这一概念则更多地应用于二维平面图形。

正确理解长方体的表面积计算，是避免误区的关键。长方体的表面积计算公式为2(ab+bc+ca)，其中a、b、c分别代表长方体的长、宽、高。这个公式准确地反映了长方体所有六个面的面积之和。

计算公式的推导

长方体的表面积计算公式2(ab+bc+ca)的推导，基于长方体六个面的面积计算。长方体的每一对面都是矩形，且面积相等。因此，我们可以先计算三组对面中每一组的面积，然后将它们相加，再乘以2，即可得到长方体的总表面积。

具体推导过程如下：

1. 计算前面和后面的面积：前面和后面的面积相等，均为长a乘以宽b，即ab。

2. 计算左面和右面的面积：左面和右面的面积相等，均为宽b乘以高c，即bc。

3. 计算上面和下面的面积：上面和下面的面积相等，均为长a乘以高c，即ca。

将以上三组面积相加，得到长方体六个面的总面积为ab+bc+ca，再乘以2，即得到长方体的表面积公式2(ab+bc+ca)。

实际应用

长方体的表面积计算，在日常生活和工业生产中有着广泛的应用。

在建筑行业，计算长方体形状的建筑物的表面积，对于材料采购、成本预算以及施工计划都至关重要。无论是房屋的外墙面积计算，还是室内装修中墙面涂料的用量估算，都离不开长方体表面积的计算。

在包装行业，长方体形状的包装盒是常见的包装形式。计算包装盒的表面积，有助于确定包装材料的用量，优化包装设计，降低成本。

此外，长方体的表面积计算还广泛应用于家具设计、机械制造、航空航天等领域。在这些领域中，精确计算长方体的表面积，对于产品设计、材料选择、成本控制等方面都具有重要意义。

数学思维的拓展

长方体的表面积计算，不仅是一个简单的数学公式应用，更是数学思维的拓展和深化。

首先，长方体的表面积计算，体现了从二维到三维的思维跨越。从平面几何中的长方形周长计算，到立体几何中的长方体表面积计算，是一个从平面到立体的思维升级。这种升级，要求我们不仅要掌握基本的数学运算技能，更要具备空间想象能力和三维几何思维。

其次，长方体的表面积计算，锻炼了我们的逻辑推理能力和问题解决能力。通过推导长方体表面积的计算公式，我们学会了如何运用已知条件，通过逻辑推理，得出未知结论。这种能力，不仅在数学学习中至关重要，更在日常生活中发挥着重要作用。

此外，长方体的表面积计算，还启示我们如何运用数学知识解决实际问题。通过将数学知识与实际问题相结合，我们可以发现数学在日常生活中的广泛应用，从而激发学习数学的兴趣和动力。

结语

长方体的周长计算，虽然在实际应用中更多地被表述为表面积的计算，但其背后所蕴含的数学知识和数学思维，却值得我们深入探究。通过理解长方体的基本概念，正确区分周长和表面积的概念，掌握表面积的计算公式及其推导过程，我们可以更好地将数学知识应用于实际问题中。同时，通过长方体的表面积计算，我们还可以锻炼自己的空间想象能力、逻辑推理能力和问题解决能力，从而在数学学习和日常生活中取得更好的成绩和表现。

长方体的周长计算，不仅是一个数学问题，更是一个数学思维的拓展和深化。它教会我们如何运用数学知识解决实际问题，如何在解决问题的过程中培养自己的数学素养和思维能力。因此，我们应该珍视这一看似简单实则深刻的数学问题，从中汲取数学知识和智慧的养分，不断提升自己的数学素养和综合能力。