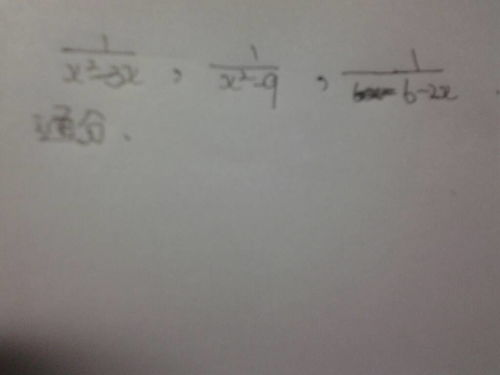如何确定最简公分母的方法？

如何确定最简公分母

在数学学习中，特别是在处理分数运算时，我们经常需要找到一个共同的分母，以便进行加减运算。这个共同的分母被称为公分母，而最简公分母则是所有公分母中分母因式最少、各因式指数最小的一个。确定最简公分母是解决分数加减问题的关键步骤，下面将详细介绍确定最简公分母的方法。

一、理解公分母的概念

首先，我们需要明确什么是公分母。当两个或多个分数需要进行加减运算时，为了计算方便，我们需要将它们转化为同分母的形式。这个共同的分母就是公分母。例如，对于分数1/2和1/3，它们的公分母可以是6，因为6是2和3的最小公倍数。

二、确定最简公分母的步骤

1. 分解质因数

确定最简公分母的第一步是将所有分母进行质因数分解。质因数分解是将一个正整数表示为若干个质数相乘的形式。例如，对于分母12和18，我们可以将它们分解为质因数：12=2×2×3，18=2×3×3。

2. 找出所有独立出现的质因数

在质因数分解后，我们需要找出所有独立出现的质因数。这些质因数将构成最简公分母的基础。例如，在上面的例子中，独立出现的质因数有2和3。

3. 将各质因数的最高次幂相乘

接下来，我们需要将各质因数的最高次幂相乘。这是因为最简公分母需要包含所有分母中出现的质因数，并且每个质因数的指数应为这些质因数在所有分母中出现的最高次数。例如，对于分母12和18，质因数2的最高次幂是2（在12=2×2×3中），质因数3的最高次幂是3（在18=2×3×3中）。因此，最简公分母为2×2×3×3=36。

4. 验证结果

最后，我们需要验证得到的结果是否确实是最简公分母。验证的方法是将原分数转化为以这个公分母为分母的形式，然后检查它们是否能够正确地进行加减运算。如果运算结果正确，那么这个公分母就是最简公分母。

三、注意事项

1. 避免重复计算

在确定最简公分母时，要注意避免重复计算质因数。每个质因数只应计算一次，并且其指数应为在所有分母中出现的最高次数。

2. 考虑特殊情况

有时，分母可能包含小数或带分数。在这种情况下，我们需要先将它们转化为假分数（即分子和分母都是整数的分数），然后再进行质因数分解和确定最简公分母。

3. 简化结果

在得到最简公分母后，有时我们还需要对运算结果进行简化。这是因为在进行加减运算后，得到的分数可能不是最简形式。此时，我们需要对分子和分母进行约分，以得到最简分数。

四、示例分析

为了更好地理解确定最简公分母的方法，我们可以分析一些具体的示例。

示例1：计算1/4+1/6。

步骤：

将分母4和6进行质因数分解：4=2×2，6=2×3。

找出所有独立出现的质因数：2和3。

将各质因数的最高次幂相乘：2×2×3=12。

将原分数转化为以12为分母的形式：1/4=3/12，1/6=2/12。

进行加法运算：3/12+2/12=5/12。

示例2：计算2/5-3/10。

步骤：

将分母5和10进行质因数分解：5=5，10=2×5。

找出所有独立出现的质因数：2和5。

将各质因数的最高次幂相乘：2×5=10。

将原分数转化为以10为分母的形式：2/5=4/10。

进行减法运算：4/10-3/10=1/10。

示例3：计算3/8+1/12。

步骤：

将分母8和12进行质因数分解：8=2×2×2，12=2×2×3。

找出所有独立出现的质因数：2和3。

将各质因数的最高次幂相乘：2×2×2×3=24。

将原分数转化为以24为分母的形式：3/8=9/24，1/12=2/24。

进行加法运算：9/24+2/24=11/24。

五、实际应用

确定最简公分母的方法在分数运算中具有广泛的应用。它不仅适用于简单的分数加减运算，还适用于复杂的分数混合运算（包括乘除和加减混合运算）。此外，在确定最简公分母的过程中，我们还可以学习到质因数分解、约分等重要的数学技能。这些技能在数学学习和日常生活中都具有重要的作用。

六、总结

确定最简公分母是解决分数加减问题的关键步骤。通过质因数分解、找出所有独立出现的质因数、将各质因数的最高次幂相乘以及验证结果等步骤，我们可以准确地找到最简公分母。在掌握了这个方法后，我们可以更加轻松地进行分数加减运算，并提高自己的数学能力。同时，确定最简公分母的方法还可以帮助我们更好地理解数学中的质因数分解、约分等概念，为后续的数学学习打下坚实的基础。

通过以上介绍和分析，相信读者已经对确定最简公分母的方法有了全面而深入的了解。在未来的数学学习中，我们可以运用这个方法来解决各种分数加减问题，不断提高自己的数学素养和解题能力。