正方形对角线长度的简单计算方法

正方形是一种具有四条等长边和四个直角的四边形。在几何学中，正方形是一种非常基础且重要的形状，其性质被广泛研究和应用。在正方形中，对角线是一个重要的概念，它不仅连接了正方形的两个对角顶点，还体现了正方形的一些重要性质。那么，正方形对角线究竟是怎么计算的呢？

首先，我们需要明确正方形的定义和性质。正方形有四条等长的边，每个角都是直角。假设正方形的边长为a，那么它的四条边的长度都是a。正方形的对角线连接了正方形的两个对角顶点，它是一条穿越正方形内部的线段。

要计算正方形的对角线长度，我们可以利用勾股定理。勾股定理是几何学中的一个基本定理，它表明在一个直角三角形中，直角边的平方和等于斜边的平方。即，如果直角三角形的两条直角边长度分别为b和c，斜边长度为d，则有b²+c²=d²。

在正方形中，我们可以构造一个由正方形的两条相邻边和一条对角线构成的直角三角形。在这个直角三角形中，两条直角边就是正方形的边长，即a，而斜边就是对角线。因此，我们可以将勾股定理应用到这个直角三角形中，来求解对角线的长度。

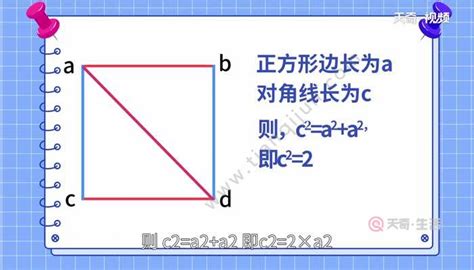
根据勾股定理，正方形的对角线d的长度可以通过以下公式计算：d²=a²+a²。这是因为正方形的两条相邻边都是a，所以两条直角边的长度都是a。将a²+a²合并同类项，我们得到d²=2a²。最后，对等式两边同时开平方根，得到d=√(2a²)=a√2。

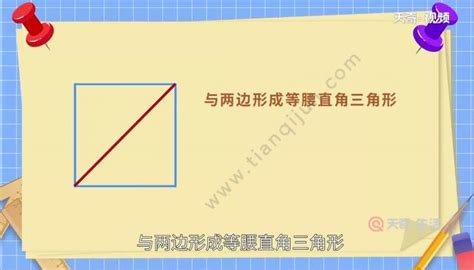
所以，正方形的对角线长度等于边长a乘以根号2。这个公式是计算正方形对角线长度的基本方法，它利用了正方形的性质和勾股定理。

在实际应用中，我们只需要知道正方形的边长，就可以利用这个公式快速计算出对角线的长度。例如，如果正方形的边长是4厘米，那么我们可以将a=4代入公式d=a√2中，得到d=4√2厘米。同样地，如果正方形的边长是5厘米，那么对角线长度就是5√2厘米。

除了利用勾股定理计算正方形的对角线长度外，我们还可以通过其他方法来验证这个结果。例如，我们可以使用几何图形的相似性质或者三角函数的性质来推导对角线的长度。这些方法虽然路径不同，但最终都会得到相同的结果，即正方形的对角线长度等于边长乘以根号2。

此外，正方形的对角线还具有一些重要的性质。例如，正方形的对角线互相垂直平分且相等。这意味着正方形的两条对角线不仅长度相等，而且它们还互相垂直，并且平分对方。这些性质使得正方形在几何学中具有独特的地位和应用价值。

在计算正方形对角线长度的过程中，我们还需要注意一些细节和注意事项。首先，要确保给定的边长是准确的，因为边长的准确性直接影响到对角线长度的计算结果。其次，在计算过程中要注意数学符号和运算规则的正确使用，以避免出现计算错误。最后，在将计算结果应用到实际问题中时，还需要考虑实际情况和条件对计算结果的影响。

正方形对角线的计算在几何学、建筑学、工程学等领域都有广泛的应用。例如，在建筑设计中，我们需要计算正方形的对角线长度来确定建筑物的尺寸和布局。在工程学中，正方形对角线的计算可以帮助我们确定某些结构件的尺寸和位置。此外，在科学研究和技术应用中，正方形对角线的计算也是不可或缺的一部分。

总的来说，正方形对角线的计算是一个简单而重要的几何问题。通过利用勾股定理和其他数学方法，我们可以轻松地求解出正方形的对角线长度。同时，正方形的对角线还具有一些重要的性质和应用价值，这使得它在几何学和相关领域中具有广泛的应用前景。

因此，当我们需要计算正方形的对角线长度时，可以灵活地运用上述方法和技巧来求解。无论是在学习、工作还是日常生活中，掌握正方形对角线的计算方法都将为我们提供便利和帮助。同时，通过对正方形对角线的研究和应用，我们也可以更深入地理解几何学的魅力和价值所在。