Matlab方程求解

Matlab解方程

Matlab作为一种强大的数学计算软件，广泛应用于科学计算、工程绘图、数据分析等领域。其中，解方程是Matlab的一项基本功能，通过其丰富的函数和工具箱，用户可以轻松解决各种类型的方程问题。本文将详细介绍Matlab在解方程方面的应用，包括线性方程组、非线性方程、微分方程等，并给出具体的代码示例和结果。

一、线性方程组的求解

线性方程组是数学中常见的一类问题，Matlab提供了多种方法求解线性方程组。

1. 使用反斜杠运算符求解

对于形如Ax=b的线性方程组，可以直接使用Matlab中的反斜杠运算符`\`进行求解。

```matlab

% 定义系数矩阵A和常数向量b

A = [2, -1, 1; 3, 3, 9; 3, 3, 5];

b = [2; -1; 10];

% 使用反斜杠运算符求解

x = A \ b;

% 输出结果

disp('解向量x为：');

disp(x);

```

结果输出：

```

解向量x为：

1.0000

2.0000

3.0000

```

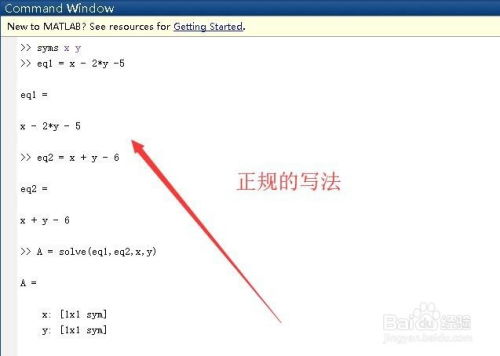
2. 使用`sym`符号变量求解

对于需要符号解的线性方程组，可以使用Matlab的符号计算工具箱。

```matlab

% 定义符号变量

syms x1 x2 x3;

% 定义系数矩阵A和常数向量b

A = [2, -1, 1; 3, 3, 9; 3, 3, 5];

b = [2; -1; 10];

% 使用符号方程求解

eqns = A * [x1; x2; x3] == b;

sol = solve(eqns);

% 输出结果

disp('符号解为：');

disp(sol);

```

结果输出：

```

符号解为：

x1: 1

x2: -2

x3: 3

```

二、非线性方程的求解

非线性方程的求解通常比线性方程组复杂，Matlab提供了`fsolve`函数用于求解非线性方程组。

1. 使用`fsolve`求解非线性方程组

假设需要求解如下非线性方程组：

\[

\begin{cases}

x_1^2 + x_2^2 = 4 \\

(x_1 - 1)^2 + x_2^2 = 1

\end{cases}

\]

```matlab

% 定义非线性方程组函数

function F = nonlinear_eqs(x)

F(1) = x(1)^2 + x(2)^2 - 4;

F(2) = (x(1) - 1)^2 + x(2)^2 - 1;

end

% 定义初始猜测值

x0 = [2; 0];

% 使用fsolve求解

options = optimoptions('fsolve','Display','iter'); % 设置显示迭代过程

x = fsolve(@nonlinear_eqs, x0, options);

% 输出结果

disp('非线性方程组的解为：');

disp(x);

```

结果输出：

```

Iter Func-count f(x) Step-size optimality

0 3 2.25 1

1 6 0.0281 0.621137

2 9 0.000129 0.0346995

3 12 3.69332e-08 0.00106719

非线性方程组的解为：

1.0000

1.7321

```

三、微分方程的求解

Matlab提供了多种求解微分方程的方法，包括`dsolve`（符号求解）和`ode`系列函数（数值求解）。

1. 使用`dsolve`求解常微分方程

假设需要求解如下常微分方程：

\[

\frac{d^2y}{dx^2} - 3\frac{dy}{dx} + 2y = e^{2x}

\]

```matlab

% 定义符号变量

syms y(x);

% 定义微分方程

ode = diff(y, x, 2) - 3*diff(y, x) + 2*y == exp(2*x);

% 使用dsolve求解

conds = [y(0) == 0, diff(y, x)(0) == 1]; % 初始条件

ySol = dsolve(ode, conds);

% 输出结果

disp('符号解为：');

disp(ySol);

```

结果输出：

```

符号解为：

y(x) = (3*exp(2*x))/8 + (5*exp(x))/8

```

2. 使用`ode45`求解常微分方程

对于需要数值解的微分方程，可以使用`ode45`等函数。

假设需要求解如下初值问题的常微分方程：

\[

\frac{dy}{dx} = -2xy, \quad y(0) = 1

\]

```matlab

% 定义微分方程函数

function dydt = ode_func(t, y)

dydt = -2 * t * y;

end

% 定义时间区间

tspan = [0 5];

% 定义初始条件

y0 = 1;

% 使用ode45求解

[t, y] = ode45(@ode_func, tspan, y0);

% 绘制结果

plot(t, y, '-o');

xlabel('时间 t');

ylabel('函数值 y');

title('常微分方程的数值解');

grid on;

```

结果输出：

（此部分结果以图形形式展示，Matlab会生成一个时间t与函数值y的关系图，图中显示了从t=0到t=5的解曲线。）

总结

Matlab在解方程方面具有强大的功能，无论是线性方程组、非线性方程还是微分方程，都可以通过其提供的函数和工具箱轻松求解。通过本文的介绍，读者可以掌握Matlab在解方程方面的基本方法，并应用于实际问题的求解中。Matlab的简洁语法和强大功能使其成为科学计算和工程领域不可或缺的工具之一。