角速度与角度变化的关系

角速度和角度的关系是物理学中一个基础且重要的概念，它涉及到旋转运动的基本描述和分析。在深入探讨这一关系之前，我们首先需要明确几个关键术语：角速度、角度以及它们之间的相互作用。

角速度是描述物体绕某点旋转快慢的物理量，通常用希腊字母ω（Omega）表示。它是一个矢量，既有大小又有方向，大小等于单位时间内转过的角度，方向与转动平面垂直，遵循右手螺旋定则。在日常生活中，我们经常会遇到角速度的概念，比如汽车轮胎的旋转、风力发电机的叶片转动等。角速度的大小决定了旋转运动的快慢，是分析旋转物体动态特性的重要参数。

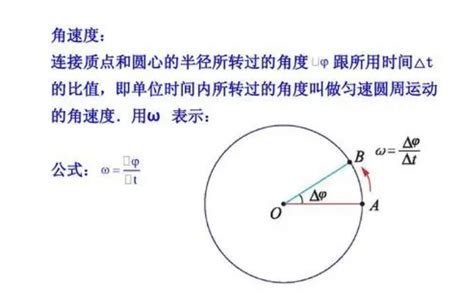
角度则是用来度量平面角大小的单位，通常用度（°）或弧度（rad）来表示。在几何学中，角度是衡量两条射线从同一点出发所夹的平面角大小的量度。角度的大小直接影响到旋转物体所扫过的面积和路径长度，是理解旋转运动的基础。

角速度和角度之间的关系可以通过一个简单的公式来表达：ω=Δθ/Δt，其中ω表示角速度，Δθ表示在Δt时间内转过的角度变化量。这个公式揭示了角速度是角度变化率的度量，即单位时间内角度的变化量。换句话说，角速度描述了旋转物体在单位时间内扫过的角度大小。

在实际应用中，我们可以通过测量旋转物体在一定时间内转过的角度来计算其角速度。例如，在一个匀速圆周运动中，物体每秒钟转过的角度是恒定的，因此其角速度也是恒定的。我们可以通过计时器和角度测量仪器来精确测量物体在一定时间内转过的角度，从而计算出其角速度。

值得注意的是，角速度和角度之间的关系在不同的旋转运动中可能表现出不同的特性。在匀速圆周运动中，角速度是恒定的，角度随时间线性增加。然而，在非匀速圆周运动中，角速度可能会随时间变化，导致角度随时间的变化呈现非线性关系。因此，在分析旋转运动时，我们需要根据具体情况来选择合适的数学模型和计算方法。

除了角速度和角度之间的关系外，我们还可以进一步探讨它们与其他物理量之间的关系。例如，在圆周运动中，线速度和角速度之间存在密切的关系：v=ωr，其中v表示线速度，r表示旋转半径。这个公式告诉我们，在旋转半径一定的情况下，线速度随角速度的增大而增大；反之，在角速度一定的情况下，线速度随旋转半径的增大而增大。这一关系在物理学和工程学中有广泛的应用，比如汽车轮胎的转速与车速的关系、风力发电机的叶片长度与转速的关系等。

此外，角加速度也是描述旋转运动的一个重要物理量。它表示角速度随时间的变化率，通常用α表示。在旋转物体受到外力矩作用时，会产生角加速度，导致角速度发生变化。角加速度与角速度之间的关系可以通过牛顿第二定律在旋转运动中的类比形式——转动定律来描述：M=Iα，其中M表示外力矩，I表示转动惯量，α表示角加速度。这个公式揭示了外力矩是产生角加速度的原因，而转动惯量则决定了物体对角加速度的抵抗能力。

在探讨角速度和角度的关系时，我们还需要注意一些特殊情况。比如，在刚体绕定轴转动的问题中，由于刚体内部各点的角速度相同，因此我们可以通过测量刚体上某一点的角速度来代表整个刚体的角速度。然而，在计算刚体的动能或动量矩时，我们需要考虑刚体的质量和形状分布，即转动惯量的影响。

此外，在处理非匀速圆周运动时，我们可能需要采用微积分的方法来描述角速度和角度之间的关系。因为此时角速度不再是恒定的，而是随时间变化的函数。我们需要通过积分来计算物体在一定时间内转过的总角度，或者通过微分来描述角速度随时间的变化率。

综上所述，角速度和角度的关系是物理学中一个基础且重要的概念。它们之间通过简单的公式相互关联，揭示了旋转运动的基本特性和规律。在实际应用中，我们需要根据具体情况来选择合适的数学模型和计算方法，以便更准确地描述和分析旋转运动。同时，我们还需要注意角速度与线速度、角加速度等物理量之间的关系，以及特殊情况下的处理方法。通过这些探讨和分析，我们可以更深入地理解角速度和角度的关系在物理学和工程学中的应用价值。