利用几何画板创建毕达哥拉斯树的步骤

几何画板是一款功能强大的数学绘图软件，它不仅能够帮助用户绘制各种几何图形，还能够通过迭代等功能生成复杂的图案。毕达哥拉斯树，作为一种基于勾股定理的几何图形，因其独特的视觉效果和数学内涵而受到广泛关注。下面，我们就来详细讲解如何使用几何画板绘制毕达哥拉斯树。

一、准备工作

首先，确保你的电脑上已经安装了几何画板软件。如果还没有安装，可以从官方网站或其他可信渠道下载并安装。安装完成后，打开几何画板，准备开始绘制毕达哥拉斯树。

二、绘制初始图形

1. 新建文件：在几何画板中，点击“文件”菜单，选择“新建”，创建一个新的几何画板文件。

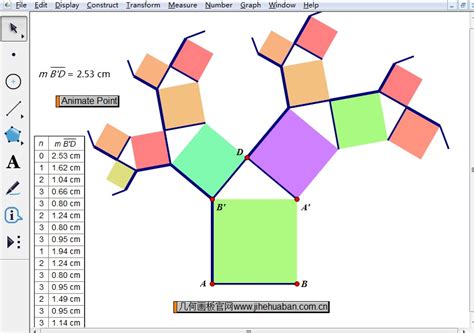
2. 绘制线段AB：使用“点工具”在画布上绘制两个点A和B，然后使用“线段工具”连接这两个点，得到线段AB。

3. 标记旋转中心：双击点A，将点A标记为旋转中心。

4. 旋转点B：选中点B，点击“变换”菜单，选择“旋转”命令。在弹出的对话框中，设置旋转角度为90度，点击“旋转”按钮。这样，点B就会围绕点A旋转90度，得到新的点B'。

5. 标记新的旋转中心：双击点B'，将点B'标记为新的旋转中心。

6. 旋转点A：选中点A，再次点击“变换”菜单，选择“旋转”命令。在弹出的对话框中，设置旋转角度为-90度（或选择顺时针旋转90度），点击“旋转”按钮。这样，点A就会围绕点B'旋转-90度，得到新的点A'。

7. 绘制线段AB'和B'A'：使用“线段工具”分别连接点A和点B'、点B'和点A'，得到线段AB'和B'A'。

三、构造中点与圆

1. 构造中点C：选中线段B'A'，点击“构造”菜单，选择“中点”命令。这样，线段B'A'的中点C就会被绘制出来。

2. 绘制圆C：依次选中点C和点A'，点击“构造”菜单，选择“以圆心和圆周上点绘圆”命令。这样，以点C为圆心、点A'到点C的距离为半径的圆C就会被绘制出来。

四、构造弧与点

1. 构造圆上的弧：选中点A'、B'和圆C，点击“构造”菜单，选择“圆上的弧”命令。这样，以点A'和点B'为端点、位于圆C上的一段弧就会被绘制出来。

2. 构造弧上的点D：保持弧的选中状态，点击“构造”菜单，选择“弧上的点”命令。这样，弧上的任意一点D就会被绘制出来。

五、隐藏与设置

1. 隐藏部分对象：选中圆C、点C、半圆弧以及线段A'B'，点击鼠标右键，选择“隐藏”命令。这样，这些对象就会被隐藏起来，不会干扰后续的绘制工作。

2. 设置线段线型：选中线段BA'，点击鼠标右键，选择“属性”命令。在弹出的对话框中，将线型设置为粗线，以便更好地突出显示。

六、度量与填充

1. 度量线段B'D的长度：构造线段B'D并选中它，点击“度量”菜单，选择“距离”命令。这样，线段B'D的长度就会被度量出来并显示在画布上。

2. 填充四边形ABA'B'的内部：选中点A、B、A'、B'，点击“构造”菜单，选择“四边形内部”命令。这样，四边形ABA'B'的内部就会被填充起来。

3. 设置填充颜色：选中四边形ABA'B'的内部以及线段B'D的长度（或直接在画布上选中填充区域），点击“显示”菜单，选择“颜色”→“参数”命令。在弹出的对话框中，采用默认设置（或根据需要调整颜色参数），然后点击“确定”按钮。这样，填充区域的颜色就会被设置完成。

七、添加动画与迭代

1. 添加动画按钮：选中点D，点击“编辑”菜单，选择“操作类按钮”→“动画”命令。在弹出的对话框中，设置动画方向为“向前”（或根据需要选择其他方向），然后点击“确定”按钮。这样，一个控制点D运动的动画按钮就会被添加到画布上。

2. 设置迭代：选中点A和点B（或选中整个初始图形），点击“变换”菜单，选择“迭代”命令。在弹出的对话框中，依次点击B'、D点作为迭代的第一对映射点。然后，点击“结构”菜单下的“添加新的映射”命令，再依次点击点D、A'作为迭代的第二对映射点。在“显示”选项中，可以增加或减少迭代的次数以观察不同的图案效果。最后，点击“迭代”按钮即可开始迭代过程并生成毕达哥拉斯树图案。

八、观察与调整

1. 观察图案变化：点击动画按钮或调整迭代次数后，观察生成的毕达哥拉斯树图案的变化。你可以通过调整迭代次数、改变动画速度或方向等方式来探索不同的图案效果。

2. 调整细节：如果需要调整图案的细节（如颜色、线型等），可以选中相应的对象并使用鼠标右键选择“属性”命令进行修改。另外，你也可以通过隐藏或显示某些对象来更好地展示图案的某些部分。

通过以上步骤，你就可以使用几何画板成功绘制出毕达哥拉斯树图案了。这个图案不仅具有独特的视觉效果，还蕴含着深刻的数学内涵和美学价值。希望你在绘制过程中能够享受到数学与艺术的完美结合带来的乐趣！