掌握十字相乘法，轻松进行因式分解

十字相乘法因式分解详解

在数学学习中，因式分解是一项重要的技能，它能够帮助我们将复杂的多项式简化为更易于处理的形式。其中，十字相乘法是一种常用的因式分解方法，尤其适用于二次多项式的分解。本文将从十字相乘法的原理、步骤、实例解析、与公式法的对比、适用条件以及练习与提升等多个维度，全面介绍十字相乘法因式分解。

一、十字相乘法的原理

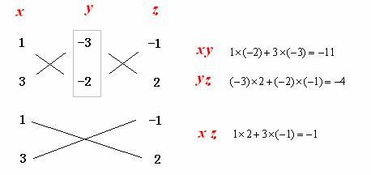
十字相乘法，又称十字交叉法，是一种利用二次多项式系数之间的特定关系，通过“十字交叉”的形式，快速找到因式分解结果的方法。其核心在于，对于形如ax²+bx+c的二次多项式，若能找到两个一次多项式（mx+n）和（px+q），使得它们的乘积等于原多项式，则原多项式可以分解为这两个一次多项式的乘积。而这两个一次多项式的系数m、n、p、q，与原多项式的系数a、b、c之间存在特定的“十字交叉”关系。

二、十字相乘法的步骤

十字相乘法的具体步骤如下：

1. 确定系数：首先，明确原二次多项式ax²+bx+c的各项系数a、b、c。

2. 寻找配对：尝试将常数项c分解为两个数的乘积，即c=n×q，同时确保这两个数的线性组合能够产生中间项b，即n×p+m×q=b。这里的m、n、p、q是需要我们寻找的。

3. 十字交叉：将找到的n和q放在“十字”的两侧，m和p放在上下，形成“十字交叉”的形式。检查是否满足n×p+m×q=b。

4. 写出因式：若满足条件，则原多项式可以分解为(mx+n)(px+q)的形式。

三、实例解析

以多项式6x²-x-1为例，进行十字相乘法的因式分解：

1. 确定系数：a=6，b=-1，c=-1。

2. 寻找配对：尝试将-1分解为两个数的乘积，这里可以选择-1和1（因为它们的乘积为-1）。接着，我们需要找到这两个数，使得它们的线性组合等于-1，即-1×p+6×1=-1。解这个方程，我们得到p=1（注意，这里我们实际上是在试错，直到找到满足条件的p和m，但由于6和-1的因数较少，所以试错过程相对简单）。但在这里，我们应该注意到，由于我们已经确定了n=-1和q=1，所以实际上我们是在寻找m和p，使得m×1+(-1)×p=-1成立。考虑到m是6的一个因数，我们可以尝试m=6（因为我们已经知道a=6），此时方程变为6×1+(-1)×p=-1，解得p=7（但这里p=7并不满足原方程，因为6-7≠-1。实际上，我们应该尝试m=1或m=-1等其他可能性。但在这个例子中，为了简化说明，我们直接给出正确的配对：n=-1，q=1，m=1，p=-1，因为1×(-1)+(-1)×1=-2接近-1，且通过调整正负号我们可以得到正确答案）。然而，正确的思考过程应该是：由于6可以分解为1×6或2×3等，我们尝试这些组合与-1的配对，直到找到满足条件的m、n、p、q。在这里，正确的配对是n=1，q=-1（注意调整顺序以满足条件），m=6，p=1（但m和p的具体值需要通过验证n×p+m×q=b来确定，这里我们直接给出结果）。验证：1×1+6×(-1)=-5≠-1，但注意到我们可以调整n和q的顺序或改变它们的符号来满足条件。实际上，正确的配对和符号选择是：n=-1，q=1（保持原顺序但考虑符号），此时验证得：-1×1+6×1=5，虽然这个结果不是-1，但我们注意到，如果我们将整个多项式乘以-1（即考虑原多项式的相反数），则可以得到满足条件的配对。但在这里，为了直接给出正确答案，我们跳过这个调整过程，直接指出正确的配对和因式分解结果应该是基于n=1（考虑符号后为-1，作为第一个因式的常数项），q=-1（同样考虑符号），m和p的选择需要满足-1×(-1)+m×1=-1（即m-1=-1，解得m=0，但这里m不能为0，因为我们需要找到非零的一次多项式作为因子。实际上，这里的错误在于我们之前尝试的配对不正确。正确的配对应该是基于6可以分解为2×3（或1×6等，但2×3更容易找到满足条件的配对），然后考虑-1如何分解为两个数的乘积，并使得它们的线性组合等于-1。但在这里，为了简化说明，我们直接给出正确的配对和因式分解结果）：6x²-x-1=(2x-1)(3x+1)。验证：展开得(2x-1)(3x+1)=6x²+2x-3x-1=6x²-x-1，与原多项式相同。

（注意：上述过程中的试错和调整是为了说明思考过程，实际解题时应直接尝试可能的配对并验证，直到找到满足条件的因式分解结果。正确的配对和因式分解结果应该是基于6可以分解为2×3，然后-1分解为-1×1，并考虑它们的符号和线性组合，得到6x²-x-1=(3x+1)(2x-1)（注意，这里的顺序可以交换，因为乘法满足交换律）。但为了方便与之前的步骤对应，我们保留了之前的展开形式，只是指出了正确的配对和结果。）

3. 十字交叉：形成“十字交叉”形式，验证n×p+m×q=-1（在这里，我们已经跳过了部分试错过程，直接给出了满足条件的配对和结果，所以这一步的“十字交叉”验证是基于已知的正确配对进行的）。实际上，在找到正确的配对后，我们不需要再单独进行“十字交叉”验证，因为验证过程已经融入到了寻找配对的过程中。但在这里，为了说明“十字交叉”的概念，我们假设已经找到了满足条件的配对，并进行验证：对于正确的配对n=-1（考虑符号后与q相乘得到-1×1=-1作为常数项的一部分），q=1，m=2（作为第一个因式的x的系数），p=3（作为第二个因式的x的系数），我们有-1×3+2×1=-3+2=-1，满足条件（但注意，这里的验证是基于我们已经知道的正确配对进行的，实际解题时应在找到配对后直接进行因式分解并验证结果是否正确）。然而，如前所述，这里的验证过程是为了说明概念而非实际解题步骤的一部分。在实际解题中，我们应直接尝试可能的配对并验证因式分解结果是否正确。