揭秘电学奥秘：深入解读基尔霍夫第二定律

基尔霍夫第二定律，作为电路理论中的一项基本定律，是分析和计算复杂电路不可或缺的工具。这一定律，也被称为基尔霍夫电压定律（KVL），其核心思想在于描述电路中任意闭合回路中各电压降与电压升的代数和为零。为了深入理解这一概念，我们可以从基尔霍夫第二定律的起源、定义、应用以及其在电路分析中的重要性等方面进行详细探讨。

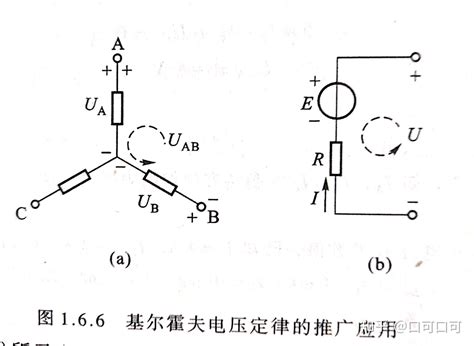
首先，回顾电路理论的发展历程，基尔霍夫定律是由德国物理学家古斯塔夫·基尔霍夫在19世纪40年代提出的。他基于电荷守恒原理和能量守恒原理，推导出了两条电路基本定律，即基尔霍夫第一定律（KCL）和基尔霍夫第二定律（KVL）。这两条定律为电路分析奠定了坚实的理论基础，使得复杂电路的分析和计算成为可能。

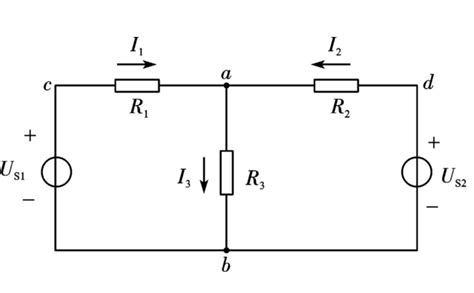
基尔霍夫第二定律，或KVL，表述为：在任一瞬时，沿闭合回路，电压降的代数和等于电压升的代数和，或者说，在一个闭合回路中，各元件上的电压代数和为零。这里的“电压降”指的是电流通过电阻、电感等元件时产生的电压损失，而“电压升”则指的是如电源等元件提供的电压增益。需要注意的是，在应用KVL时，必须明确电压的参考方向，并确保在计算过程中遵循代数运算的规则。

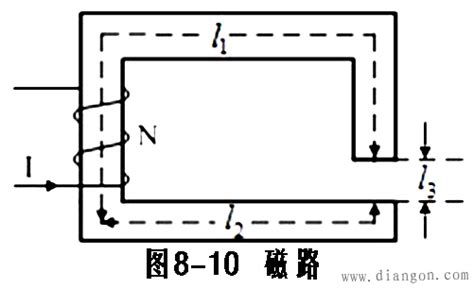
为了直观理解KVL，我们可以考虑一个简单的直流电路，其中包含一个电源和两个电阻。在这个电路中，电流从电源的正极流出，经过第一个电阻产生电压降，然后流过第二个电阻再次产生电压降，最后返回电源的负极。根据KVL，我们可以列出该电路的电压方程，即电源电压等于两个电阻上电压降之和。通过解这个方程，我们可以得到电路中的电流值，进而分析电路的其他参数。

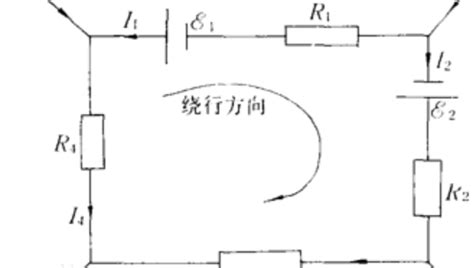
KVL的应用不仅仅局限于直流电路，它还广泛适用于交流电路、动态电路以及含有非线性元件的复杂电路。在交流电路中，电压和电流都是随时间变化的，但KVL仍然成立，只不过此时的电压和电流需要用复数形式表示，以体现它们的相位关系。在动态电路中，电感和电容等储能元件的存在使得电路分析变得更为复杂，但KVL仍然是一个有力的分析工具。它可以帮助我们建立电路的微分方程，进而求解电路中的暂态过程。

在含有非线性元件的电路中，KVL同样适用，但此时电路的分析可能需要采用数值方法或近似方法。非线性元件的电压-电流关系不再是线性关系，因此电路的行为可能表现出多种稳定性态，如周期振荡、混沌等。在这些情况下，KVL仍然是电路分析的基础，但需要结合其他理论和方法进行深入研究。

KVL在电路分析中的重要性不仅体现在其广泛的应用范围上，还体现在它与其他电路理论之间的联系上。例如，在求解电路中的功率问题时，我们可以利用KVL列出电路的电压方程，然后结合欧姆定律和功率公式求解。在求解含有受控源的电路时，KVL同样是一个有力的工具。受控源是一种特殊的电源，其输出电压或电流受电路中其他支路电压或电流的控制。通过应用KVL，我们可以将受控源看作普通元件进行处理，从而简化电路的分析过程。

此外，KVL还与电路的拓扑性质密切相关。电路的拓扑性质指的是电路元件之间的连接关系，它决定了电路的基本结构和行为。KVL实际上是对电路拓扑性质的一种数学描述。在电路分析和设计中，我们经常需要改变电路的拓扑结构以满足特定的需求。例如，在电源变换电路中，我们可能需要通过增加或减少电路元件来改变电路的输出电压或电流。在这个过程中，KVL可以帮助我们确保新电路仍然满足基本的电压约束条件。

在实际应用中，KVL还具有许多重要的工程意义。例如，在电力系统的分析和设计中，我们需要考虑电力系统的稳定性和可靠性。KVL可以帮助我们分析电力系统中的电压分布和电压稳定性问题，从而采取相应的措施来提高电力系统的性能。此外，在电子电路的设计和测试中，KVL也是一个重要的测试依据。通过测量电路中的电压值并与理论值进行比较，我们可以验证电路的正确性和可靠性。

综上所述，基尔霍夫第二定律作为电路理论中的一项基本定律，具有广泛的应用范围和重要的工程意义。它描述了电路中任意闭合回路中各电压降与电压升的代数和为零的关系，为电路分析提供了有力的工具。在应用KVL时，我们需要明确电压的参考方向并遵循代数运算的规则。通过深入研究KVL在直流电路、交流电路、动态电路以及含有非线性元件的复杂电路中的应用，我们可以更好地理解电路的行为和特性，为电路的分析和设计提供有力的支持。同时，KVL还与电路的拓扑性质密切相关，为电力系统的稳定性和可靠性分析以及电子电路的设计和测试提供了重要的理论依据。