二进制与十进制互转详解:转换方法与步骤
在数字世界的奇妙旅程中,二进制与十进制如同两位语言不通却又能和谐共舞的舞者,它们各自拥有独特的韵律与节奏,却能在需要时无缝转换,共同编织出数字宇宙的斑斓画卷。想象一下,你是一位探险家,踏入了这片由0和1构成的神秘领域,准备揭开二进制与十进制之间转换的奥秘。那么,就让我们一同踏上这场既烧脑又充满乐趣的探索之旅吧!

探索起点:二进制世界的奥秘
首先,我们来到的是二进制的世界——一个由最简单的元素0和1构建起来的宇宙。在这里,没有复杂的数值体系,只有这两种基本符号在不断排列组合中创造出无限可能。二进制之所以如此重要,是因为它是计算机内部信息存储和处理的基石。无论是你的手机屏幕上的每一个像素点,还是服务器中飞速流转的数据包,背后都是二进制的默默支撑。

从二进制到十进制:解码数字的魔法
现在,让我们学习如何像侦探一样,从二进制的迷宫中解读出十进制的真相。想象一下,你手里拿着一串二进制数,比如`1011`,它就像是一个待解的密码,而你的任务就是找到它对应的十进制数值。

解密步骤:
1. 从左到右,位值加权:二进制中的每一位都有一个权重,从右往左分别是`2^0, 2^1, 2^2, ...`。对于`1011`,最右边的`1`代表`2^0`,向左依次是`2^1`、`2^2`、`2^3`。

2. 对应位相乘再求和:接下来,将二进制数中每个1所在位置的权重值相乘,然后将这些乘积相加。对于`1011`:
第一位(最右边)的1乘以`2^0 = 1`
第二位的0不参与计算(因为任何数与0相乘都是0)
第三位的1乘以`2^1 = 2`
第四位的1乘以`2^2 = 4`
将这些值相加得到`1 + 0 + 2 + 4 = 7`,所以`1011`(二进制)等于`7`(十进制)。
从十进制到二进制:编织数字的奇迹
接下来,让我们逆向而行,从熟悉的十进制世界穿越到二进制的世界。这个过程就像是用0和1的丝线,编织出一幅幅精美的图案。
编织步骤:
1. 不断除以2,取余数:将十进制数不断除以2,记录下每次除法的余数,直到商为0。这些余数(从最后一次除法开始)按顺序排列,就是对应的二进制数。
2. 逆序排列:由于我们是从商为0开始记录的,所以需要将得到的余数序列逆序排列,才能得到正确的二进制数。
举个例子,将十进制数`23`转换为二进制:
`23 ÷ 2 = 11 ... 余 1`
`11 ÷ 2 = 5 ... 余 1`
`5 ÷ 2 = 2 ... 余 1`
`2 ÷ 2 = 1 ... 余 0`
`1 ÷ 2 = 0 ... 余 1`
逆序排列这些余数:`10111`,所以`23`(十进制)等于`10111`(二进制)。
数字转换的趣味应用
掌握了二进制与十进制之间的转换技巧,你就像拥有了一把解锁数字世界奥秘的钥匙。这些技能在日常生活中或许不常直接用到,但在计算机科学、编程、网络通信等领域却是不可或缺的基础。比如,了解二进制的转换能帮助你更好地理解计算机内存的工作原理,或是让你在调试程序时能够更准确地定位问题。
此外,二进制与十进制的转换还是一种锻炼逻辑思维和数学能力的好方法。它要求你在抽象的概念之间建立联系,通过不断的练习,你的大脑将变得更加灵活和敏锐。
结语
在这场从二进制到十进制,再从十进制回归二进制的探索之旅中,我们不仅学习了数字转换的技巧,更深刻体会到了数字世界的奇妙与和谐。二进制与十进制,这两个看似截然不同的体系,在数字的世界里却能够如此完美地相互转换,共同支撑起现代科技的繁荣与发展。下次当你面对一串复杂的数字时,不妨试着用这两种语言去解读它,或许你会发现,数字的世界比你想象的要更加丰富多彩。
-
 二进制转换为十进制的方法资讯攻略11-10
二进制转换为十进制的方法资讯攻略11-10 -
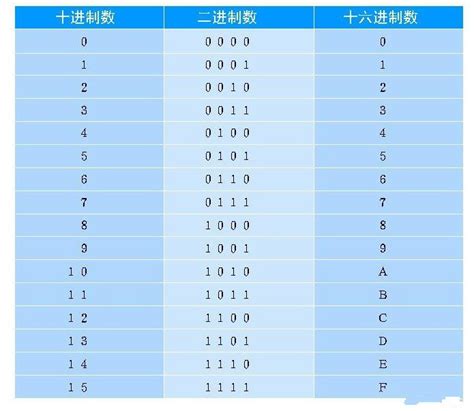 揭秘:十进制数变身二进制数的神奇转换法资讯攻略12-08
揭秘:十进制数变身二进制数的神奇转换法资讯攻略12-08 -
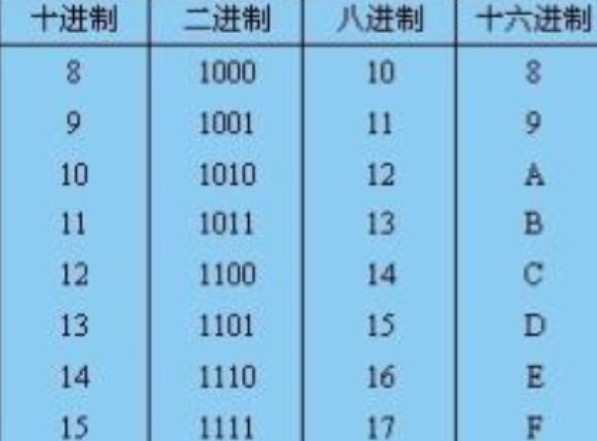 十六进制转换方法资讯攻略11-26
十六进制转换方法资讯攻略11-26 -
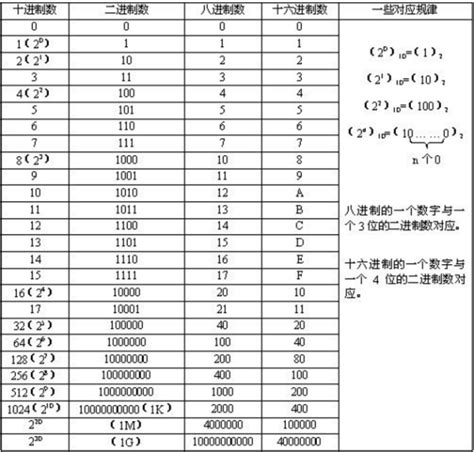 轻松掌握:16进制转10进制的方法资讯攻略12-03
轻松掌握:16进制转10进制的方法资讯攻略12-03 -
 二进制转十进制与十进制转二进制的方法是什么?资讯攻略10-24
二进制转十进制与十进制转二进制的方法是什么?资讯攻略10-24 -
 十六进制转二进制的详细方法资讯攻略11-07
十六进制转二进制的详细方法资讯攻略11-07