揭秘!轻松掌握钝角三角形高的神秘画法,让几何学习不再犯难
在探讨如何绘制钝角三角形的高这一几何问题时,我们首先需要明确几个基本概念:钝角三角形是三角形中一个角大于90°的三角形,而三角形的高则是从三角形的一个顶点垂直到它的对边(或对边的延长线)上的一条线段。由于钝角三角形的特殊性,其高的绘制方式相较于锐角或直角三角形会有所不同,这主要体现在高可能落在三角形的外部。下面,我们将从多个维度详细阐述如何绘制钝角三角形的高。

一、理解基础概念
1.1 钝角三角形的定义
钝角三角形是三角形中最为直观的一种特殊形态,它至少包含一个大于90°的角。这个特点决定了其至少有一边相对于其他两边来说更长,从而影响了高的绘制位置。
1.2 高的定义与性质
三角形的高是连接顶点与对边(或对边延长线)的垂直线段。在钝角三角形中,由于存在大于90°的角,至少有一条高会落在三角形的外部。这一性质是理解并准确绘制钝角三角形高的关键。

二、绘制步骤详解
2.1 确定顶点与对边
首先,明确你想要从哪个顶点出发绘制高。在钝角三角形中,无论选择哪个顶点,都需要找到其对应的对边。这一步是绘制高的基础。
2.2 使用直尺与量角器(或视觉判断)
直尺:用于绘制直线段,包括高本身和可能需要的辅助线。
量角器(或视觉判断):虽然绘制高本身不直接需要量角器,但了解哪些角是钝角,以及如何通过视觉判断垂直位置,对于准确绘制高至关重要。
2.3 绘制高
从顶点出发:使用直尺,从选定的顶点出发,轻轻画一条线段,注意这条线段将作为高的起点。
寻找垂足:接下来,需要找到这条线段与对边(或其对边延长线)的垂足。在钝角三角形中,如果顶点与对边之间的连线不直接相交于对边上,则需要延长对边,直到与从顶点出发的线段垂直相交。
完成绘制:当垂足确定后,连接顶点与垂足,即完成了从该顶点出发的高的绘制。
三、实践案例与注意事项
3.1 实践案例
假设我们有一个钝角三角形ABC,其中∠C为钝角。若我们想从顶点A出发绘制高,步骤如下:
1. 确定顶点A和对边BC。
2. 使用直尺从A点出发,轻轻画一条指向BC方向的线段作为辅助。
3. 延长BC边(如果A到BC的连线不与BC相交),直到这条辅助线与BC的延长线垂直相交于点D。
4. 连接A点与D点,得到的高AD即为从顶点A出发的钝角三角形ABC的高。
3.2 注意事项
准确性:确保高是垂直的,这是绘制高的基本要求。
延长线的理解:理解并正确绘制对边的延长线,对于钝角三角形中某些高的绘制至关重要。
灵活应用:根据具体情况选择合适的顶点作为高的起点,因为钝角三角形中不同顶点出发的高可能落在三角形的不同位置(内部或外部)。
四、教学意义与拓展
4.1 教学意义
掌握钝角三角形高的绘制方法,不仅是对几何基础知识的巩固,更是培养学生空间想象能力和逻辑推理能力的重要途径。通过实际操作,学生可以更直观地理解三角形高的概念,以及它在几何证明和计算中的应用。
4.2 拓展应用
面积计算:知道如何绘制三角形的高后,可以利用底乘高除以2的公式来计算三角形的面积,这在解决实际问题时非常有用。
几何证明:在复杂的几何证明中,钝角三角形的高常常作为辅助线出现,帮助构建证明所需的平行线、垂直线等关系。
生活应用:在建筑、测量等领域,三角形高的概念也有广泛应用,如确定建筑物的高度、测量坡度等。
结语
综上所述,绘制钝角三角形的高是一个既基础又富有挑战性的几何任务。通过理解基本概念、掌握绘制步骤、注意实践中的细节以及思考其教学意义和拓展应用,我们可以更加全面而深入地掌握这一知识点。在几何的世界里,每一个细节都蕴含着无限的奥秘和可能,等待着我们去探索和发现。
- 上一篇: 揭秘'衙内'一词背后的真正含义,你了解多少?
- 下一篇: 轻松解答!如何快速开通云闪付的手机闪付功能?
-
 【一秒辨别】钝角、锐角、直角大不同,你真的会分吗?资讯攻略10-25
【一秒辨别】钝角、锐角、直角大不同,你真的会分吗?资讯攻略10-25 -
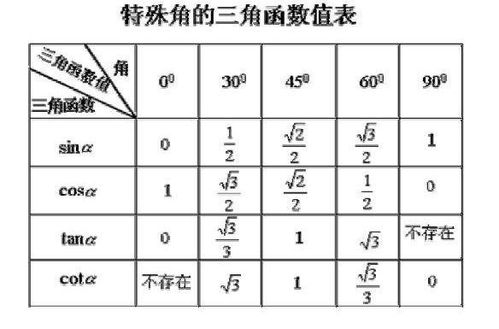 三角函数常见公式概览资讯攻略11-28
三角函数常见公式概览资讯攻略11-28 -
 揭秘:掌握五种绝妙技巧,轻松判定三角形全等!资讯攻略01-17
揭秘:掌握五种绝妙技巧,轻松判定三角形全等!资讯攻略01-17 -
 掌握6种创意平行线画法,轻松提升绘画技能!资讯攻略11-24
掌握6种创意平行线画法,轻松提升绘画技能!资讯攻略11-24 -
 等腰三角形:对称之美的几何诠释资讯攻略11-17
等腰三角形:对称之美的几何诠释资讯攻略11-17 -
 揭秘!《黑神话悟空》幽魂BOSS终极打法全攻略,轻松过关不犯难!资讯攻略10-18
揭秘!《黑神话悟空》幽魂BOSS终极打法全攻略,轻松过关不犯难!资讯攻略10-18











