揭秘：arcsinx与sinx分之一，它们真的是等价的吗？

arcsinx并不等于sinx分之一

在数学的世界里，符号和公式构成了其独特的语言，每一个符号背后都承载着特定的数学意义。对于初学者来说，“arcsinx”和“sinx分之一（即1/sinx）”这两个表达式看起来似乎有些相似，容易让人产生混淆。然而，事实上，这两者之间有着本质的区别。本文将从定义、图像、性质和应用四个方面，详细解析arcsinx与1/sinx的不同，帮助大家准确理解这两个数学表达式的真正含义。

一、定义上的区别

1. arcsinx的定义

arcsinx，即反正弦函数，是正弦函数sinx的反函数。在数学上，如果一个函数f(x)在某个区间内是单调的，并且它的值域是另一个区间内的所有数，那么在这个区间内，f(x)的反函数就存在。对于正弦函数sinx，在区间[-π/2, π/2]内，它是单调递增的，并且值域为[-1,1]。因此，在这个区间内，我们可以定义sinx的反函数为arcsinx，即满足sin(arcsinx) = x，且x∈[-1,1]。

2. 1/sinx的定义

1/sinx，即正弦函数的倒数，表示的是正弦函数sinx在某个点上的值的倒数。它是一个新的函数，与sinx和arcsinx在定义上完全不同。对于任意x（除了使得sinx=0的点，即x=kπ，k为整数），1/sinx都有定义。

二、图像上的区别

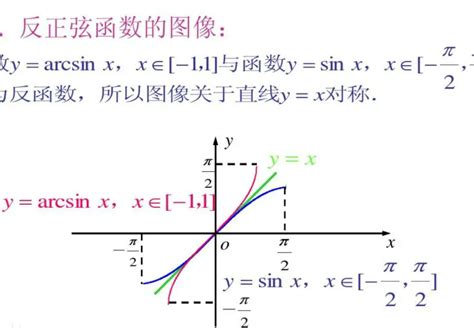
1. arcsinx的图像

arcsinx的图像是一个在原点为中心、形状类似于正弦函数但经过翻转和伸缩变换后的图像。由于arcsinx的定义域为[-1,1]，值域为[-π/2, π/2]，因此其图像是一个在这个矩形区域内的连续曲线。这个曲线在y轴两侧是对称的，且在x=-1和x=1处分别达到其最小值和最大值。

2. 1/sinx的图像

1/sinx的图像则更为复杂。由于sinx在x=kπ（k为整数）处为0，因此1/sinx在这些点处没有定义，即图像上会出现断点或无穷大/无穷小的点。在除了这些点以外的其他点上，1/sinx的图像呈现出周期性的波动，每个周期内都有一个正的极大值和一个负的极小值。这些极大值和极小值分别对应于sinx的极小值和极大值的倒数。

三、性质上的区别

1. arcsinx的性质

奇函数性质：arcsinx是奇函数，即arcsin(-x) = -arcsinx。

单调性：在定义域[-1,1]内，arcsinx是单调递增的。

值域：arcsinx的值域为[-π/2, π/2]。

导数：arcsinx的导数为1/√(1-x²)，在定义域内恒大于0（除了端点-1和1处为无穷大）。

2. 1/sinx的性质

奇偶性：1/sinx是奇函数，即1/sin(-x) = -1/sinx（在定义域内）。

周期性：1/sinx是周期函数，周期为2π。

无界性：在x=kπ（k为整数）处，1/sinx无定义或趋于无穷大/无穷小。

导数：1/sinx的导数为-cosx/(sin²x)，在定义域内变化复杂。

四、应用上的区别

1. arcsinx的应用

角度计算：在几何和物理问题中，经常需要计算给定正弦值对应的角度，这时可以使用arcsinx函数。

信号处理：在信号处理领域，arcsinx常用于相位恢复和频率分析等任务中。

工程计算：在工程计算中，如结构分析、控制系统设计等，arcsinx也经常被用作求解非线性方程的工具。

2. 1/sinx的应用

电路分析：在电路分析中，特别是在交流电路的计算中，1/sinx函数（或其相关形式）有时被用于描述电流、电压等物理量的变化关系。

波动分析：在波动分析中，如声波、光波等的传播和反射问题中，1/sinx函数有时被用于描述波动特性的变化。

特殊函数计算：在数学和物理学中，1/sinx函数作为特殊函数的一种，有时被用于求解复杂方程或计算特定积分等问题中。

综上所述，arcsinx与1/sinx在定义、图像、性质和应用等方面都存在显著的差异。