十六进制转二进制的详细方法

十六进制转换成二进制，是数字转换中的一项基础而重要的技能。在计算机科学、电子工程和数据分析等领域，我们常常需要将十六进制数转换为二进制数，以便进行进一步的处理和分析。下面，我们就来详细探讨一下十六进制如何转换成二进制的方法，以及与之相关的一些基本概念和注意事项。

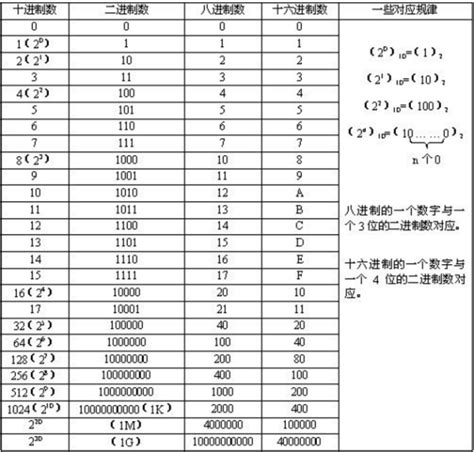
首先，我们要了解十六进制和二进制的基本概念。十六进制，简称Hex，是一种基数为16的数制。它使用0到9的数字和A到F的字母来表示数值，其中A表示10，B表示11，C表示12，D表示13，E表示14，F表示15。二进制，则是一种基数为2的数制，它只使用0和1两个数字来表示数值。在计算机内部，所有的信息都是以二进制的形式存储和处理的。

那么，如何将十六进制数转换为二进制数呢？其实，这个过程可以通过两种主要的方法来实现：直接转换法和间接转换法。

直接转换法，就是将十六进制数的每一位直接转换成相应的二进制数。由于十六进制数的每一位可以表示4位的二进制数（因为2的4次方等于16），所以我们可以根据十六进制数的每一位的值，找到对应的4位二进制数。例如，十六进制数的1位A，对应的二进制数就是1010；1位F，对应的二进制数就是1111。然后，我们将这些二进制数按照十六进制数的位序排列起来，就得到了转换后的二进制数。

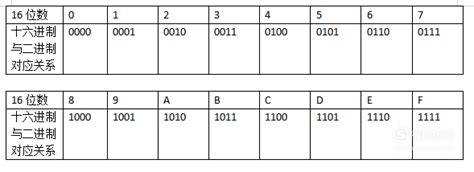
举个例子，如果我们有一个十六进制数3A7F，我们就可以直接将它转换成二进制数。首先，我们将3转换成二进制数0011，将A转换成二进制数1010，将7转换成二进制数0111，将F转换成二进制数1111。然后，我们将这些二进制数按照3A7F的位序排列起来，就得到了转换后的二进制数0011101001111111。

当然，直接转换法虽然直观易懂，但在处理较长的十六进制数时可能会比较繁琐。这时，我们可以采用间接转换法来简化操作。

间接转换法，就是先将十六进制数转换成十进制数，然后再将十进制数转换成二进制数。这种方法利用了十进制数作为中间桥梁，将十六进制数和二进制数之间的转换问题转化为了两个相对简单的问题。

首先，我们将十六进制数转换成十进制数。这个过程类似于我们将十进制数转换成其他数制的过程，只不过我们需要将每一位上的数值乘以对应的权重（16的幂次方），然后将这些乘积相加得到结果。例如，十六进制数3A7F转换成十进制数的过程就是：3*16^3+A*16^2+7*16^1+F*16^0=15007。

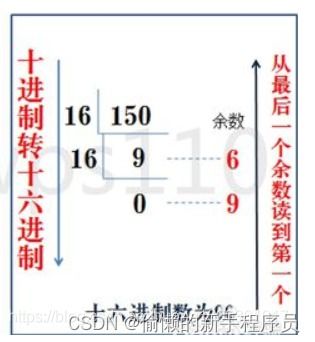
然后，我们将得到的十进制数转换成二进制数。这个过程可以通过“除2取余法”来实现。我们将十进制数除以2，得到商和余数；然后，将商再次除以2，得到新的商和余数；如此反复进行，直到商为0为止。最后，我们将所有的余数按照从后往前的顺序排列起来，就得到了转换后的二进制数。

例如，我们将十进制数15007转换成二进制数的过程就是：15007/2=7503余1，7503/2=3751余1，3751/2=1875余1，1875/2=937余1，937/2=468余1，468/2=234余0，234/2=117余0，117/2=58余1，58/2=29余0，29/2=14余1，14/2=7余0，7/2=3余1，3/2=1余1，1/2=0余1。然后，我们将所有的余数按照从后往前的顺序排列起来，就得到了转换后的二进制数11101001111111。

需要注意的是，虽然间接转换法在处理较长的十六进制数时可能会比直接转换法更加简便，但它也引入了额外的计算步骤和误差风险。因此，在选择转换方法时，我们需要根据具体的情况和需求来进行权衡和选择。

此外，还有一些其他的注意事项和技巧可以帮助我们更好地进行十六进制到二进制的转换。例如，我们可以利用十六进制数的特性和规律来简化计算过程；我们可以使用计算器或编程语言中的内置函数来快速进行转换；我们还可以参考相关的资料和教程来加深对转换方法和原理的理解和掌握。

总的来说，十六进制转换成二进制是数字转换中的一项基础而重要的技能。通过掌握直接转换法和间接转换法这两种主要的方法以及相关的注意事项和技巧，我们可以更加高效、准确地进行十六进制到二进制的转换工作。同时，这也可以为我们进一步学习和掌握计算机科学、电子工程和数据分析等领域的相关知识