自然数的定义与解析
自然数,这个看似简单却充满奥秘的数学概念,自古以来就是人类探索数学世界的基石之一。它们是我们日常生活中最直观、最常用的数字,从数数、计数到更复杂的数学运算,自然数都扮演着不可或缺的角色。那么,什么是自然数?它们又是如何被定义、分类和应用的呢?

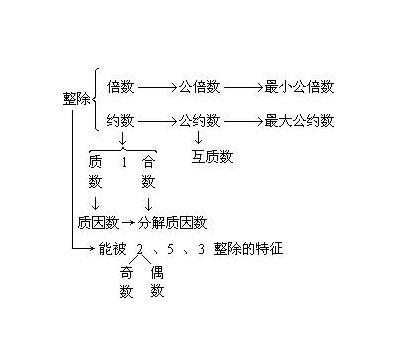
首先,从定义上来看,自然数是指用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4……所表示的数。自然数由0开始,一个接一个,组成一个无穷的集体。自然数有有序性,无限性。分为偶数和奇数,合数和质数等。自然数集N是指表示物体个数的数,包括0、1、2、3、4……在数学上,使用符号N来表示自然数集,而N+或N*则表示不包括0的自然数集,有时也使用ℕ₊或ℕ*来表示这个集合。
自然数的有序性,是指每个自然数都有一个后继者,记为n+1,例如,1的后继者是2,2的后继者是3等等。同时,每个自然数除了0以外,都有且仅有一个前驱者,例如,3的前驱者是2,2的前驱者是1等等。这种有序性使得自然数可以进行大小的比较和排序,从而构成了数学中的序数理论。
自然数的无限性,则是指自然数集是一个无穷无尽的集合,它包含了无限多个自然数。这种无限性使得自然数可以进行无限制的加、减、乘、除等运算,从而构成了数学中的算术理论。同时,自然数的无限性也使得数学中的极限理论得以建立和发展。
在自然数的分类中,偶数和奇数是两种最基本的分类方式。偶数是指能够被2整除的自然数,如0、2、4、6等;而奇数则是指不能被2整除的自然数,如1、3、5、7等。偶数和奇数在数学中有着重要的地位,它们在数的性质、运算规律以及数学问题的解决中都有着广泛的应用。
除了偶数和奇数外,自然数还可以按照其因数个数进行分类,得到合数和质数两种分类方式。合数是指除了1和它本身外还有其他因数的自然数,如4、6、8等;而质数则是指只有1和它本身两个因数的自然数,如2、3、5等。质数是数学中的一个重要概念,它们在数论、密码学等领域都有着广泛的应用。
自然数的应用是广泛的,它们不仅在数学中有着重要的地位,而且在物理学、化学、生物学、经济学等各个领域都有着广泛的应用。在物理学中,自然数被用来描述物体的数量、位置和运动状态等;在化学中,自然数被用来表示原子的序数、分子的组成和化学反应的计量关系等;在生物学中,自然数被用来描述生物体的数量、种类和遗传信息等;在经济学中,自然数被用来表示商品的数量、价格和市场供求关系等。
在数学中,自然数的应用更是无处不在。它们是数学运算的基础,无论是加、减、乘、除还是更复杂的运算,都离不开自然数。同时,自然数也是数学理论的重要组成部分,如数论、代数、几何等各个领域都离不开自然数的支持和应用。在数论中,自然数被用来研究数的性质、分布和规律等;在代数中,自然数被用来表示变量的取值范围、方程的解和函数的定义域等;在几何中,自然数被用来描述图形的数量、形状和位置关系等。
此外,自然数还与数学中的其他重要概念密切相关。例如,自然数与整数、有理数和无理数等数学概念之间有着密切的联系和区别。整数包括自然数、0和负整数,它们构成了数学中的整数集;有理数则包括整数和分数,它们可以表示成两个整数的比;而无理数则是不能表示成两个整数的比的数。这些数学概念之间既有联系又有区别,它们共同构成了数学中的数系理论。
除了数学中的应用外,自然数还与人类的思维和文化密切相关。在人类的历史长河中,自然数一直扮演着重要的角色。它们是人类认识世界、改造世界的重要工具之一。在古代文明中,如古埃及、古巴比伦和中国等,人们就已经开始使用自然数进行计数和运算。随着数学的发展,自然数的应用范围不断扩大,它们在各个领域都发挥着重要的作用。
在现代社会中,自然数的应用更是无处不在。随着计算机和信息技术的飞速发展,自然数在数据处理、网络通信和信息安全等领域发挥着越来越重要的作用。同时,自然数也成为了人们日常生活中不可或缺的一部分,如电话号码、邮政编码、身份证号码等都离不开自然数的支持和应用。
综上所述,自然数是一个既简单又复杂的数学概念。它们既是数学运算的基础又是数学理论的重要组成部分;既是人类认识世界的重要工具又是现代社会中不可或缺的一部分。因此,我们应该深入学习和理解自然数的概念和性质以及它们在数学和各个领域中的应用价值。只有这样,我们才能更好地利用自然数这个强大的工具来认识世界、
- 上一篇: 如何在中国邮政查询挂号信状态
- 下一篇: 如何让文件夹安全无忧?轻松加密技巧揭秘!
-
 互质数:详细解析与定义资讯攻略11-01
互质数:详细解析与定义资讯攻略11-01 -
 橡实:定义与解析资讯攻略11-30
橡实:定义与解析资讯攻略11-30 -
 精油SPA按摩的定义与解析资讯攻略11-22
精油SPA按摩的定义与解析资讯攻略11-22 -
 瓷贴面的定义与解析资讯攻略12-06
瓷贴面的定义与解析资讯攻略12-06 -
 装修中的'地台'定义及其安装后的实用功能资讯攻略11-13
装修中的'地台'定义及其安装后的实用功能资讯攻略11-13 -
 揭秘:空镜头与定镜头的定义及实用用途资讯攻略12-01
揭秘:空镜头与定镜头的定义及实用用途资讯攻略12-01












