施密特正交化计算方法详解
施密特正交化的计算

施密特正交化(Gram-Schmidt Orthogonalization)是一种将一组线性无关向量正交化的方法。正交化后的向量组不仅线性无关,而且两两正交,即它们的点积为零。这种方法在许多数学和工程应用中非常有用,特别是在求解线性方程组、特征值问题和数值积分等领域。下面详细介绍施密特正交化的计算步骤和过程。
假设我们有一个线性无关的向量组 {v1, v2, ..., vn},目标是将其正交化为 {u1, u2, ..., un}。
步骤1:计算第一个正交向量 u1
第一个正交向量 u1 直接等于原始向量 v1,即
u1 = v1
步骤2:计算第二个正交向量 u2
第二个正交向量 u2 是通过将 v2 投影到 u1 上,然后从 v2 中减去这个投影得到的。具体计算公式为:
u2 = v2 - (v2 · u1) / (u1 · u1) * u1
其中,“·” 表示向量的点积。
步骤3:计算第三个正交向量 u3
第三个正交向量 u3 是通过将 v3 分别投影到 u1 和 u2 上,然后从 v3 中减去这些投影得到的。具体计算公式为:
u3 = v3 - (v3 · u1) / (u1 · u1) * u1 - (v3 · u2) / (u2 · u2) * u2
步骤4:依次类推,计算第n个正交向量 un
一般地,第n个正交向量 un 是通过将 vn 分别投影到 u1, u2, ..., un-1 上,然后从 vn 中减去这些投影得到的。具体计算公式为:
un = vn - Σ [(vn · ui) / (ui · ui)] * ui (i = 1, 2, ..., n-1)
其中,Σ 表示求和。
下面通过一个具体的例子来演示施密特正交化的计算过程。
例子:
假设我们有以下两个线性无关的二维向量:
v1 = [1, 2]
v2 = [2, 1]
步骤1:计算第一个正交向量 u1
u1 = v1 = [1, 2]
步骤2:计算第二个正交向量 u2
首先计算 v2 和 u1 的点积:
v2 · u1 = 2 * 1 + 1 * 2 = 4
然后计算 u1 的模的平方(即点积自身):
u1 · u1 = 1 * 1 + 2 * 2 = 5
接着计算投影系数:
(v2 · u1) / (u1 · u1) = 4 / 5
最后将投影从 v2 中减去,得到 u2:
u2 = v2 - (4 / 5) * u1 = [2, 1] - (4 / 5) * [1, 2] = [2, 1] - [4/5, 8/5] = [6/5, -3/5]
为了简化计算,我们可以将 u2 归一化(即除以其模),但这一步在施密特正交化过程中不是必须的,通常只在需要正交规范基时才进行。
结果:
u1 = [1, 2]
u2 = [6/5, -3/5] = [2 * (3/5), -1 * (3/5)] * (1/3) 的3倍 = [2, -1](已归一化)
注意: 在实际应用中,是否对正交向量进行归一化取决于具体需求。如果只需要正交向量组,那么可以省略归一化步骤;如果需要正交规范基(即每个向量的模都为1),则需要对每个正交向量进行归一化处理。
进一步扩展:三个向量的施密特正交化
假设我们再加一个向量 v3 = [1, 1],现在要对 {v1, v2, v3} 进行施密特正交化。
步骤1和步骤2:
u1 = [1, 2]
u2 = [2, -1](已归一化)
步骤3:计算第三个正交向量 u3
首先计算 v3 和 u1 的点积:
v3 · u1 = 1 * 1 + 1 * 2 = 3
计算 v3 和 u2 的点积:
v3 · u2 =
- 上一篇: 汽车点烟器该如何正确使用?
- 下一篇: 酒店退房流程是怎样的?
-
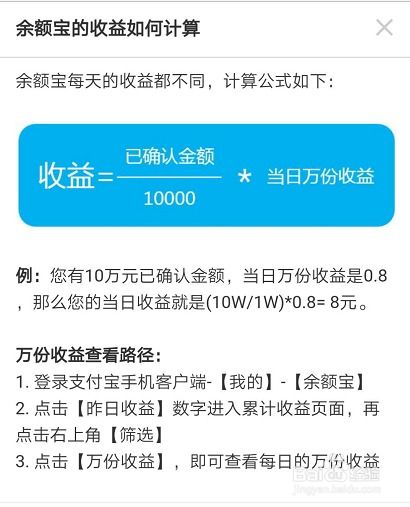 余额宝收益如何计算资讯攻略11-21
余额宝收益如何计算资讯攻略11-21 -
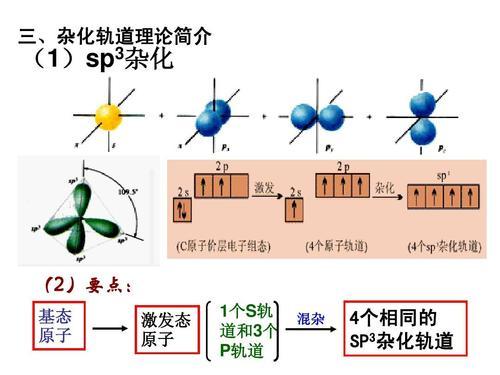 如何识别SP、SP²、SP³杂化?一文详解判别方法资讯攻略01-09
如何识别SP、SP²、SP³杂化?一文详解判别方法资讯攻略01-09 -
 掌握“七日年化收益率”,轻松计算投资收益资讯攻略11-10
掌握“七日年化收益率”,轻松计算投资收益资讯攻略11-10 -
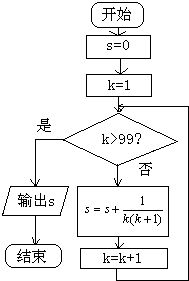 掌握12x12乘法速算技巧,轻松计算不再难!资讯攻略11-30
掌握12x12乘法速算技巧,轻松计算不再难!资讯攻略11-30 -
 揭秘《妄想山海》:化灵丹获取秘籍,助你飞升仙境的绝妙途径!资讯攻略10-23
揭秘《妄想山海》:化灵丹获取秘籍,助你飞升仙境的绝妙途径!资讯攻略10-23 -
 合格率计算方法详解资讯攻略11-23
合格率计算方法详解资讯攻略11-23












