拉格朗日定理公式详解,一看就懂!
拉格朗日定理公式是数学中一个具有深远意义的概念,它存在于多个学科领域中,并且在不同分支中有着各自独特的表现形式和应用。本文将围绕“拉格朗日定理公式是什么”这一核心问题,从微积分中的拉格朗日中值定理、群论中的拉格朗日定理以及拉格朗日乘子法等多个角度进行阐述。

微积分中的拉格朗日中值定理
拉格朗日中值定理(Lagrange's Mean Value Theorem)是微积分中的一个基本定理,它建立了函数在某区间内的平均变化率与该函数在该区间内某一点的瞬时变化率(即导数)之间的关系。定理表述如下:
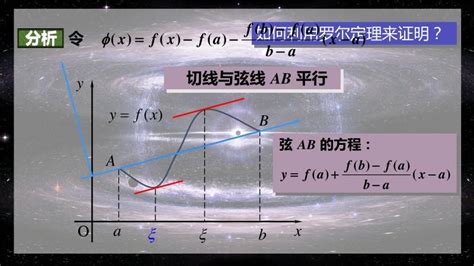
设函数y=f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,那么在开区间(a,b)内至少存在一点ξ,使得f'(ξ)=(f(b)-f(a))/(b-a)。

这里的f'(ξ)表示函数f(x)在ξ点的导数,(f(b)-f(a))/(b-a)表示函数f(x)在区间[a,b]上的平均变化率。拉格朗日中值定理不仅具有理论意义,还可以用来证明一些重要的定理,如泰勒公式、洛必达法则等。

拉格朗日中值定理的几何意义在于,如果在闭区间[a,b]上连续且可导的函数y=f(x)的图像是一条连续曲线,那么在这条曲线上至少存在一点ξ,使得该点的切线斜率等于曲线在区间[a,b]上的平均斜率。
群论中的拉格朗日定理
群论中的拉格朗日定理(Lagrange's Theorem)是有限群论中的一个基本定理,它给出了有限群的子群阶数与群阶数之间的关系。定理表述如下:
设H是有限群G的一个子群,则H的阶(即H中元素的个数)整除G的阶(即G中元素的个数)。
这一定理的证明依赖于陪集的概念。设G是一个有限群,H是G的一个子群,那么对于G中的任意元素a,可以构造出H的一个左陪集aH={ah|h∈H}。可以证明,不同的左陪集是不相交的,且G可以被分解为若干个左陪集的并集。由于每个左陪集的元素个数都等于H的元素个数,因此G的元素个数(即G的阶)可以被H的元素个数(即H的阶)整除。
拉格朗日定理在有限群论中有着广泛的应用,它不仅是许多其他定理的基础,还可以用来解决一些具体的群论问题。例如,可以利用拉格朗日定理证明一个有限群中的非单位元的阶一定整除该群的阶;还可以利用拉格朗日定理找出某些有限群的全部子群的阶数。
需要注意的是,拉格朗日定理的逆命题并不成立。即,给定一个有限群G和一个整除G的阶的整数n,并不一定有阶数为n的子群。例如,4次交替群A4没有6阶的子群。
拉格朗日乘子法
拉格朗日乘子法(Lagrange Multipliers)是数学分析中用于求解约束条件下函数极值的一种方法。该方法的核心思想是通过引入拉格朗日乘子,将约束条件与原函数结合,从而构造出一个新的函数(即拉格朗日函数),使得求解原函数的极值问题转化为求解新函数的无条件极值问题。
设函数f(x1,x2,...,xn)在定义域D内可微,且存在约束条件g(x1,x2,...,xn)=0。要求f在D内满足约束条件的极值点。可以构造拉格朗日函数L(x1,x2,...,xn,λ)=f(x1,x2,...,xn)+λg(x1,x2,...,xn),其中λ是拉格朗日乘子。然后求解方程组
{∂L/∂x1=0, ∂L/∂x2=0, ..., ∂L/∂xn=0, g(x1,x2,...,xn)=0},
得到可能的极值点。需要注意的是,得到的解需要进一步检验是否为极值点,以及是否满足约束条件。
拉格朗日乘子法在优化问题中有着广泛的应用,特别是在处理含有等式约束的优化问题时。此外,拉格朗日乘子法还可以推广到处理不等式约束的优化问题,这时需要引入拉格朗日松弛函数和KKT条件等概念。
总结
拉格朗日定理公式在不同的数学领域中有着不同的表现形式和应用。在微积分中,拉格朗日中值定理建立了函数在某区间内的平均变化率与该函数
- 上一篇: 电脑拨号上网的轻松指南:一键连接世界!
- 下一篇: 如何办理公司注册流程?
-
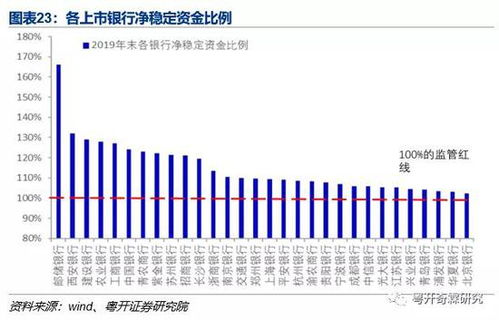 存贷比计算公式详解,一看就懂!资讯攻略10-31
存贷比计算公式详解,一看就懂!资讯攻略10-31 -
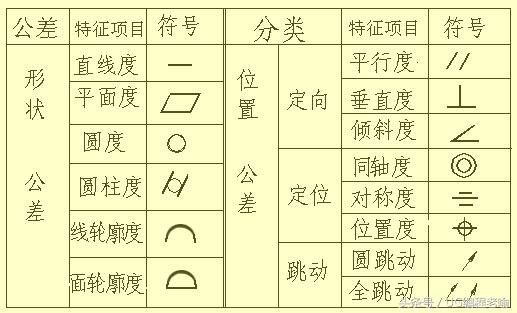 公差符号详解,一看就懂!资讯攻略12-05
公差符号详解,一看就懂!资讯攻略12-05 -
 轻松掌握!12306网上订火车票全流程图解(一看就懂)资讯攻略11-05
轻松掌握!12306网上订火车票全流程图解(一看就懂)资讯攻略11-05 -
 摇号结果查询全攻略:一看就懂的步骤指南!资讯攻略10-30
摇号结果查询全攻略:一看就懂的步骤指南!资讯攻略10-30 -
 如何正确填写政治面貌,一看就懂!资讯攻略10-31
如何正确填写政治面貌,一看就懂!资讯攻略10-31 -
 工作性质填写指南,一看就懂!资讯攻略12-02
工作性质填写指南,一看就懂!资讯攻略12-02