梯形体积怎么计算？

在几何学中，梯形是一种四边形，它有一对平行的对边，我们通常称它们为上底和下底，而另外两边则是梯形的腰。尽管梯形在二维平面上有明确的定义和性质，但在三维空间中讨论梯形的体积却稍显复杂，因为梯形本身是一个平面图形，并不具备体积属性。然而，当我们考虑一个由梯形作为底面的三维形状——梯形体（也称为台体或截头锥体）时，体积的概念就变得清晰起来。本文将从梯形体的定义、梯形体积公式的推导、梯形体积公式的应用以及与其他几何形状体积公式的比较等多个维度，来探讨梯形体积公式的相关内容。

梯形体的定义

梯形体，顾名思义，是指其底面为梯形、顶点与底面各顶点连线构成的四棱锥被平行于底面的平面所截而形成的几何体。更一般地，它也可以被视为两个相似的平行六面体（或长方体）的公共部分，其中一个六面体的底面是梯形的上底，另一个的底面是梯形的下底。这种几何体在生活中很常见，比如水桶、酒瓶等，它们的外观轮廓往往可以近似看作梯形体。

梯形体积公式的推导

要计算梯形体的体积，我们需要先理解其构成原理。梯形体可以看作是由无数个平行且等间距的梯形堆叠而成，这些梯形的面积从上到下逐渐增大（或减小），形成了一种连续的体积变化。为了简化计算，我们通常使用微积分的方法，通过积分来计算这种连续变化的体积。

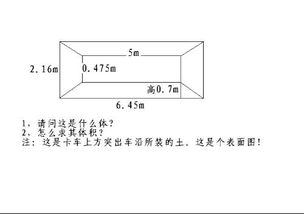
但在初等几何中，我们可以采用一种更直观且易于理解的方法来推导梯形体的体积公式。考虑一个由梯形ABCD作为底面，顶点为E（垂直于底面ABCD的某一点）的梯形体。我们可以先计算出梯形ABCD的面积S，然后乘以梯形体的高h（即点E到底面ABCD的垂直距离），但这样做会得到的是一个以梯形为底、高为h的柱体的体积，而我们需要的是梯形体（即截头锥体）的体积。

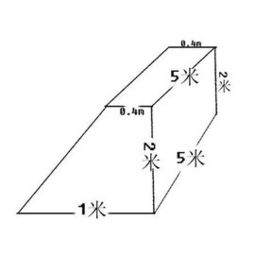
为了修正这个误差，我们引入了“相似比例”的概念。由于梯形体可以看作是两个相似的平行六面体的公共部分，因此，其体积可以通过这两个六面体体积的加权平均来得到。具体来说，如果我们把梯形ABCD的面积记作S1，梯形EFGH（假设E、F、G、H分别是EA、EB、EC、ED延长线与某一平行于ABCD的平面的交点，且该平面与ABCD平行）的面积记作S2，那么梯形体的体积V可以通过下式计算：

V = (1/3) * h * (S1 + S2 + √(S1 * S2))

这个公式的推导基于了相似三角形的性质以及体积的加权平均原理。其中，1/3的系数来自于三棱锥（四面体）的体积公式V = (1/3) * 底面积 * 高，而S1 + S2 + √(S1 * S2)则是通过加权平均的方式得到的等效底面积。

梯形体积公式的应用

梯形体积公式在生活和工程领域有着广泛的应用。例如，在建筑设计中，设计师可能需要计算不规则形状房间的体积，如果房间的形状可以近似看作梯形体，那么就可以使用梯形体积公式来进行计算。在水利工程中，计算水库或池塘的容积时，如果其形状可以近似为梯形体，同样可以使用该公式。此外，在物理学、化学等领域，当涉及到流体动力学、物质分布等问题时，梯形体积公式也可能成为解决问题的关键工具。

与其他几何形状体积公式的比较

梯形体积公式与其他几何形状（如长方体、圆柱体、圆锥体等）的体积公式既有相似之处，也有其独特之处。相似之处在于，它们都是基于几何形状的基本属性（如底面积、高）来计算体积的。而不同之处在于，梯形体积公式的推导和应用更多地涉及到了相似比例、加权平均等概念，这使得它在处理不规则形状时具有更高的灵活性和适应性。

例如，与长方体相比，梯形体的底面不是一个规则的矩形，而是一个梯形，这导致了在计算体积时需要考虑更多的因素（如上底和下底的面积差异）。与圆柱体相比，梯形体的高并不是沿着底面圆的直径方向，而是垂直于底面梯形的一个方向，这导致了在计算体积时需要考虑底面形状的变化。与圆锥体相比，虽然梯形体和圆锥体都涉及到“截头”的概念，但梯形体的底面是一个梯形而不是一个圆，这导致了在计算体积时需要采用不同的公式和方法。

结语

综上所述，梯形体积公式是一个在处理不规则形状体积问题时非常有用的工具。虽然梯形本身是一个平面图形并不具备体积属性，但由梯形作为底面的梯形体却是一个重要的三维几何体。通过理解和应用梯形体积公式，我们可以更加准确地计算和分析各种复杂形状的体积问题。同时，梯形体积公式的推导和应用也展示了数学在解决实际问题中的强大力量和魅力。无论是在日常生活、工程设计还是科学研究领域，梯形体积公式都发挥着不可替代的作用。