微分的奥秘：深度解析其几何意义

在数学的广阔天地里，微积分如同一座巍峨的山峰，不仅因其深奥的理论让人敬畏，更因其广泛的应用而深入人心。今天，我们就来聊聊微积分中的一个重要概念——微分，特别是它的几何意义，尽量用通俗易懂的语言，带大家走进这个奇妙的世界。

想象一下，你正在驾驶一辆汽车，车上的里程表显示你已经行驶了100公里。当你继续前行，行驶了一小段距离后，里程表变成了100.5公里。这0.5公里的增量，相对于100公里的总路程来说，就是一个小小的变化。在微积分中，这种微小的变化被称为“微分”。而微分的几何意义，简单来说，就是描述函数在某一点附近的小幅变化如何与它的切线相关联。

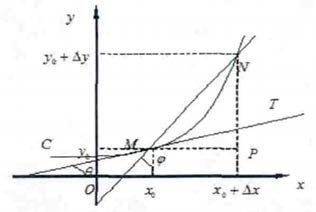
一、从直线到曲线：理解切线的概念

在几何学中，直线是最简单的图形，两点确定一条直线。但在微积分中，我们经常要面对的是曲线，它们比直线复杂得多，但微积分提供了一套强大的工具来处理这些复杂性。切线是理解微分几何意义的关键一环。在曲线上的某一点，切线是与该点“刚刚接触”的那条直线，即在该点附近，曲线与切线几乎重合。

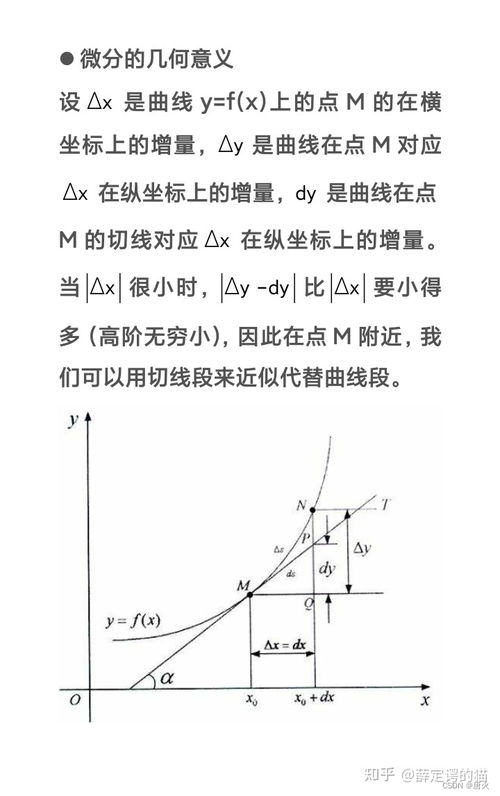
二、函数的微小变化：微分的直观感受

现在，让我们回到函数的世界。假设有一个函数y=f(x)，它描述了某个变量y如何依赖于另一个变量x。在微积分中，我们通常关心的是函数在某一点（比如x=a）处的变化率，这可以通过求导数来实现。导数，记为f'(a)，表示函数在x=a处的切线斜率，也即是函数在该点的“瞬时速度”。

微分的几何意义，就在于这个导数是如何帮助我们理解函数在一点附近的小幅变化的。想象一下，我们站在函数y=f(x)的图像上，位于点(a, f(a))。当我们沿着x轴向右移动一个微小的距离Δx时，我们的y值也会发生微小的变化Δy。这个Δy，就是函数在x=a处由于Δx引起的变化量，也就是我们要找的微分。

三、微分的几何解释：利用切线逼近

那么，这个Δy与导数f'(a)之间有什么关系呢？微分的几何意义在于，当Δx非常小时，Δy可以近似地表示为f'(a)乘以Δx，即Δy≈f'(a)Δx。这个近似是基于一个重要的原理：当Δx趋近于0时，函数在(a, f(a))点附近的图像越来越接近它的切线。因此，我们可以用切线的斜率（即导数）来近似函数在该点附近的变化率。

为了更好地理解这一点，我们可以画一个图。在函数y=f(x)的图像上，找到点(a, f(a))，然后画出该点的切线。现在，想象一个小矩形，它的底边是Δx，高是从f(a)到切线上对应于x=a+Δx的那一点的垂直距离。这个垂直距离就是我们用切线斜率近似得到的Δy的值。

四、微分的应用：从几何到现实

微分的几何意义不仅仅停留在理论层面，它在实际应用中有着广泛的用途。比如，在物理学中，速度和加速度的概念就是通过微分来定义的。速度可以看作是位置函数关于时间的微分，而加速度则是速度函数关于时间的微分。通过这些微分，我们可以理解物体在某一瞬间的运动状态。

在工程领域，微分同样发挥着重要作用。比如，在设计桥梁或建筑时，工程师需要计算材料在不同受力状态下的变形量，这通常涉及到对应力-应变关系的微分分析。此外，在经济学中，边际成本、边际收益等概念也是通过微分来描述的，它们帮助经济学家做出最优决策。

五、微分与极限：深入理解微分的本质

要深入理解微分的几何意义，我们还需要提及另一个重要的概念——极限。在微积分中，极限是理解导数和微分的基础。当我们说Δy≈f'(a)Δx时，实际上是在说，当Δx趋近于0时，Δy与f'(a)Δx之间的误差会趋近于0。这个“趋近于”的过程，就是极限的思想。

极限不仅帮助我们定义了导数，还使得我们能够精确地描述函数在一点附近的行为。通过极限，我们可以证明，对于任意给定的误差范围，总存在一个Δx的绝对值小于某个正数ε，使得当|Δx|<ε时，Δy与f'(a)Δx之间的误差小于任意给定的正数δ。这就是微分的精确性所在。

六、总结：微分，连接几何与现实的桥梁

微分的几何意义，在于它提供了一种用切线斜率来近似函数在一点附近变化量的方法。这种方法不仅简单直观，而且具有强大的理论支持和广泛的应用价值。通过微分，我们可以将复杂的曲线问题转化为简单的直线问题来处理，从而大大简化了计算和分析的过程。

更重要的是，微分架起了一座连接几何与现实世界的桥梁。无论是在物理学、工程学、经济学还是其他领域，微分都扮演着至关重要的角色。它帮助我们理解自然界和人类社会中的各种现象和规律，为人类的科技进步和社会发展提供了有力的数学工具。

因此，当我们再次面对微积分这座巍峨的山峰时，不妨以一种更加轻松和自信的心态去攀登。因为，只要我们理解了微分的几何意义，掌握了它的应用方法，就能够在这座山峰上找到属于自己的风景和收获。