解锁列举法的奥秘：三步轻松掌握

列举法作为一种经典且直观的解题策略，在数学、计算机科学、以及日常生活的问题解决中扮演着重要角色。其核心思想在于通过一一列举可能的解决方案来找出符合题目要求的答案。尽管这种方法在某些复杂情境下可能显得效率低下，但其直观性和可靠性使得它成为解决特定类型问题的首选策略。下面，我们将从列举法的三个核心步骤——明确问题、逐一列举、检验答案，来深入探讨这一方法。

明确问题：界定范围，确定标准

列举法的第一步，也是至关重要的一步，是明确问题。这要求我们不仅要清楚理解问题的具体要求，还要能够界定出问题的可能解集的范围。明确问题的过程，实际上是一个对问题进行抽象和形式化的过程，它要求我们将问题的所有关键信息提取出来，并用精确的语言加以描述。

例如，在解决“从1到100中，找出所有能被3整除的数”这一问题时，我们首先需要明确问题的范围是1到100之间的所有整数，而判断标准是这些数能否被3整除。这一步骤的准确性直接决定了后续列举工作的效率和准确性。

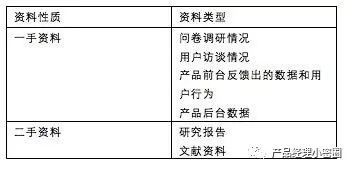
在实际操作中，明确问题还包括了对问题可能解的初步预估。这种预估有助于我们选择合适的列举策略，比如是按顺序列举，还是按某种特定的规则（如从大到小、从特殊到一般）进行列举。

逐一列举：系统排查，不遗漏不重复

在明确问题之后，接下来的任务就是逐一列举所有可能的解决方案。这一步是列举法的核心所在，它要求我们按照某种确定的顺序，系统地、全面地排查所有可能的解，确保既不遗漏任何一个可能的答案，也不重复计算。

逐一列举的过程往往是一个耗时的过程，尤其是在解集范围较大时。因此，在列举过程中，我们需要采取一些策略来提高效率。比如，对于连续整数范围的问题，我们可以按照从小到大的顺序逐一检查；对于具有某种特定规律的问题，我们可以根据规律来缩小列举范围；对于组合问题，我们可以利用排列组合的原理来减少不必要的列举。

此外，逐一列举还要求我们具备耐心和细心。因为列举法的关键在于全面性和准确性，任何一个遗漏或错误都可能导致最终答案的错误。因此，在列举过程中，我们需要时刻保持警惕，确保每一步都准确无误。

检验答案：验证解的有效性

在逐一列举出所有可能的解决方案之后，我们还需要对这些答案进行检验。检验的目的是确认这些答案是否真正符合问题的要求，以及它们是否是最优解（如果问题要求找出最优解的话）。

检验答案的过程通常包括两个步骤：一是验证每个答案是否满足问题的所有条件；二是比较不同答案之间的优劣（如果问题要求找出最优解的话）。在验证答案的过程中，我们需要回到问题的原始定义中去，用问题给出的条件或标准来检验每个答案的有效性。

值得注意的是，检验答案并不总是必需的。在某些情况下，我们可以通过列举过程本身的逻辑性和完整性来确保答案的正确性。比如，在解决一些简单的分类或计数问题时，我们只需要确保列举过程中没有遗漏或重复就可以得出正确答案。然而，在解决一些更复杂的问题时，检验答案就显得尤为重要了。

列举法的三个步骤——明确问题、逐一列举、检验答案——是一个相互关联、相互依赖的整体。明确问题是基础，它决定了列举的范围和标准；逐一列举是核心，它要求我们全面、准确地排查所有可能的解；检验答案是保障，它确保了最终答案的有效性和正确性。

在实际应用中，这三个步骤可能需要根据具体情况进行灵活调整。比如，在解决一些动态变化的问题时，我们可能需要在列举过程中不断调整问题的范围和条件；在解决一些组合优化问题时，我们可能需要在列举和检验之间反复迭代以找到最优解。然而，无论情况如何变化，列举法的核心思想——通过一一列举来找出问题的解——都是不变的。

列举法不仅是一种解题策略，更是一种思维方式。它教会我们在面对复杂问题时如何保持冷静和耐心，如何系统地思考和解决问题。通过列举法的训练和实践，我们可以培养自己的逻辑思维能力和问题解决能力，从而在未来的学习和工作中更加游刃有余。