对数螺线的参数方程转换方法
对数螺线怎么转换成参数方程

对数螺线是一种非常特殊且迷人的曲线,它在数学、物理和自然界中都有着广泛的应用。对数螺线的一个显著特点是,在任何一点上,它到原点的距离与它和该点与原点连线的夹角之间存在一定的数学关系。这一特性使得对数螺线在极坐标系下描述起来非常方便。然而,为了在某些数学问题或应用中更方便地处理对数螺线,我们可能需要将其转换为参数方程。本文将详细讨论对数螺线的性质,并逐步推导其转换为参数方程的过程。

一、对数螺线的定义与性质
对数螺线(也称为等角螺线)是一种永远向着极点绕行的螺线,越绕越靠近极点,但永远不会到达极点。这种螺线在自然界中非常普遍,如海螺壳的轮廓、旋风的形状以及某些植物的生长模式等。
在极坐标系中,对数螺线的方程可以表示为:
ρ = αe^(kφ)
其中,ρ是点到原点的距离(极径),φ是点与极轴的夹角(极角),α和k是常数,e是自然对数的底(约等于2.71828)。
对数螺线的一个重要性质是,在任何一点P上,点P到原点O的连线与点P处的切线之间的夹角α是一个定值,这个角的大小永远不会改变。这一性质使得对数螺线在旋转对称和缩放对称方面具有独特的性质。
二、参数方程的基本概念
参数方程是数学中的一种重要工具,它用一个或多个参数来描述一个曲线或曲面的形状和位置。参数方程的优点在于,它们可以方便地表示那些难以用普通方程直接描述的复杂曲线。
例如,在质点运动中,质点的位置通常与时间有关,可以表示为x=f(t),y=g(t)的形式。这里的t就是参数,它沟通了变量x和y之间的联系,为研究曲线的形状和性质提供了方便。
三、将对数螺线转换为参数方程
要将对数螺线的极坐标方程ρ = αe^(kφ)转换为参数方程,我们需要找到ρ和φ与直角坐标系中的x和y之间的关系。在极坐标系中,ρ和φ与直角坐标系中的x和y之间的关系是:
x = ρcosφ
y = ρsinφ
将对数螺线的极坐标方程代入上述关系式中,我们得到:
x = αe^(kφ)cosφ
y = αe^(kφ)sinφ
这里,φ可以作为参数,因为它在极坐标方程中是一个自由变量。通过选择不同的φ值,我们可以得到对数螺线上的一系列点,这些点连接起来就构成了对数螺线的形状。
为了更清晰地表示这个过程,我们可以将上述方程进一步简化为参数方程的形式。设t=kφ,则φ=t/k,代入上述方程中,得到:
x = αe^tcos(t/k)
y = αe^tsin(t/k)
这里,t是新的参数,它取代了原来的φ,但保持了对数螺线的所有性质。通过选择不同的t值,我们可以得到对数螺线上的任意一点。
四、参数方程的应用与优势
将对数螺线转换为参数方程后,我们可以更方便地对其进行各种数学操作和分析。以下是一些参数方程的应用和优势:
1. 简化计算:参数方程可以将复杂的曲线表示为简单的函数形式,从而简化计算过程。例如,在求曲线的长度、面积或体积时,参数方程通常比极坐标方程或普通方程更容易处理。
2. 直观理解:参数方程通过引入参数t,将曲线的形状和位置与参数t的变化联系起来。这使得我们可以更直观地理解曲线的生成过程和性质。例如,在物理问题中,参数t可以表示时间,从而帮助我们理解质点在不同时间点的位置和速度。
3. 便于绘图:参数方程可以方便地用于计算机绘图软件中,通过改变参数t的值,我们可以生成曲线的动态图像,从而更直观地观察曲线的形状和变化。
4. 解决复杂问题:对于一些复杂的曲线或曲面问题,建立它们的普通方程可能非常困难甚至不可能。而参数方程则提供了一种更为灵活和简便的方法来描述这些曲线或曲面。例如,在解决飞行器的轨迹问题时,参数方程可以方便地表示飞行器的位置、速度和加速度等参数随时间的变化关系。
五、实例分析
为了更好地理解对数螺线的参数方程及其应用,我们可以通过一个具体的实例来进行分析。
假设我们要绘制一个对数螺线的图像,并计算其长度。我们可以按照以下步骤进行操作:
1. 确定参数方程:根据前面的推导,我们得到对数螺线的参数方程为x = αe^tcos(t/k),y = αe^tsin(t/k)。在这个例子中,我们可以选择α=1,k=1来简化计算。
2. 选择参数范围:为了绘制完整的对数螺线图像,我们需要选择一个合适的参数t的范围。在这个例子中,我们可以选择t从0到10的变化范围。
3. 绘制图像:使用计算机绘图软件(如MATLAB、Python的matplotlib库等),我们可以根据参数方程绘制出对数螺线的图像。通过调整参数t的值,我们可以观察到对数螺线逐渐靠近极点的过程。
4. 计算长度:要计算对数螺线的长度,我们可以使用弧长公式L = ∫√[(dx/dt)^2 + (dy/dt)^2]dt。将参数方程代入该公式中,并进行积分计算,即可得到对数螺线的长度。
通过以上步骤,我们可以更深入地理解对数螺线的性质和应用,并掌握将其转换为参数方程的方法。
结语
对数螺线作为一种特殊的曲线,在数学、物理和自然界中都有着广泛的应用。通过将其转换为参数方程,我们可以更方便地对其进行各种数学操作和分析。本文详细讨论了将对数螺线转换为参数方程的过程和方法,并通过实例分析展示了参数方程的应用和优势。希望这些内容能够帮助读者更好地理解对数螺线的性质和应用,并在实际问题中灵活运用参数方程这一工具。
- 上一篇: 如何轻松制作一寸照片电子版
- 下一篇: 火狐浏览器怎样设置网页快捷方式?
-
 如何求解解析式?资讯攻略02-25
如何求解解析式?资讯攻略02-25 -
 探索复数的奇妙世界:概念解析与运算技巧资讯攻略11-18
探索复数的奇妙世界:概念解析与运算技巧资讯攻略11-18 -
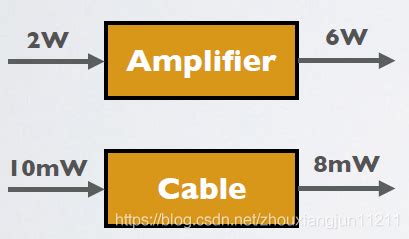 dBi与dB转换全解析资讯攻略12-04
dBi与dB转换全解析资讯攻略12-04 -
 如何创建灰度图像资讯攻略02-23
如何创建灰度图像资讯攻略02-23 -
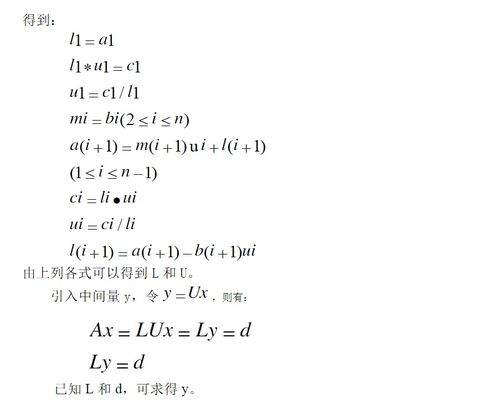 如何掌握解方程组的三种基本方法?资讯攻略11-18
如何掌握解方程组的三种基本方法?资讯攻略11-18 -
 一元二次方程的四种求解方法资讯攻略11-11
一元二次方程的四种求解方法资讯攻略11-11