Excel标准差计算详解：STDEV、STDEVA等函数怎么用？

在Excel中，标准差是一个非常重要的统计量，它用于衡量数据集的离散程度。标准差越大，表示数据点之间的差异越大；标准差越小，表示数据点越接近平均值。Excel提供了多种函数来计算标准差，其中最常见的是STDEV和STDEVA函数。本文将详细介绍Excel中标准差的计算方法，包括STDEV、STDEVA等函数的使用及其区别。

一、标准差的基本概念

标准差是方差的平方根，方差则是每个数据点与平均值之差的平方的平均值。标准差反映了数据集的离散程度，即数据点相对于平均值的波动情况。标准差的值越大，说明数据集的离散程度越高；标准差的值越小，说明数据集的离散程度越低。

二、Excel中的标准差函数

在Excel中，有多个函数可以用来计算标准差，其中最常用的是STDEV和STDEVA函数。

1. STDEV函数

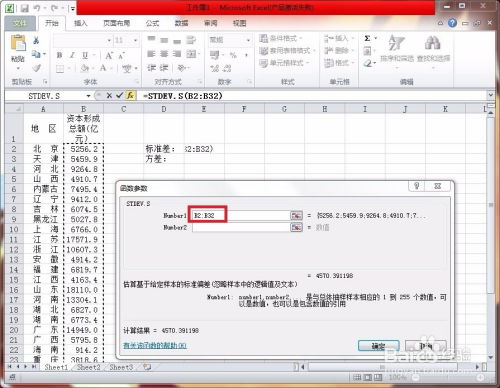
STDEV函数用于计算基于样本的标准差。如果数据集中的数据代表了一个样本（即数据集是从总体中随机抽取的一部分），则应该使用STDEV函数来计算标准差。

语法：

STDEV(number1, [number2], ...)

number1, [number2], ...：这些是代表样本数据的一系列数值或数值区域。

示例：

假设有一个数据集{2, 4, 6, 8, 10}，我们可以使用STDEV函数来计算其标准差。

=STDEV(2, 4, 6, 8, 10)

计算结果将是一个数值，表示该数据集的标准差。

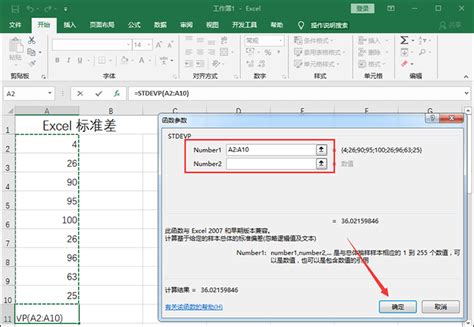
2. STDEV.P函数

虽然STDEV函数是用于计算样本标准差的，但Excel还提供了一个名为STDEV.P的函数，用于计算基于整个总体的标准差。然而，在实际应用中，我们通常更常见到的是使用STDEV函数（样本标准差），因为大多数情况下我们处理的是样本数据而非完整的总体数据。

语法：

STDEV.P(number1, [number2], ...)

number1, [number2], ...：这些是代表总体数据的一系列数值或数值区域。

注意：

尽管STDEV.P函数存在，但在日常工作中使用较少，因为大多数情况下我们处理的是样本数据。

3. STDEVA函数

STDEVA函数与STDEV函数类似，但它可以处理包含文本或逻辑值（TRUE/FALSE）的数据集。当数据集中可能包含非数值数据时（如空单元格、文本或逻辑值），STDEVA函数会忽略这些非数值数据，并计算剩余数值数据的标准差。

语法：

STDEVA(value1, [value2], ...)

value1, [value2], ...：这些是代表数据集的一系列值，可以是数值、文本或逻辑值。非数值数据将被忽略。

示例：

假设有一个数据集{2, "文本", 4, TRUE, 6, FALSE, 8}，我们可以使用STDEVA函数来计算其标准差（忽略文本和逻辑值）。

=STDEVA(2, "文本", 4, TRUE, 6, FALSE, 8)

计算结果将是一个数值，表示忽略非数值数据后的数据集的标准差。

三、使用标准差函数的注意事项

在使用STDEV、STDEVA等函数时，需要注意以下几点：

1. 数据类型一致性：确保数据集中的数据类型一致，以便准确计算标准差。如果数据集中包含非数值数据（如文本或逻辑值），请使用STDEVA函数来忽略这些数据。

2. 样本与总体的区别：明确数据是代表样本还是总体。如果数据是样本数据，请使用STDEV函数；如果数据是总体数据（虽然这种情况较少），则可以考虑使用STDEV.P函数（但通常不推荐，因为大多数情况下我们处理的是样本数据）。

3. 空单元格的处理：在Excel中，空单元格被视为缺失值，并在计算标准差时被忽略。因此，在计算标准差之前，不需要手动删除或填充空单元格。

4. 数据的代表性：确保数据集具有代表性，即能够反映总体数据的特征。如果数据集太小或不具备代表性，则计算出的标准差可能无法准确反映总体的离散程度。

5. 函数的选择：根据数据集的实际情况选择合适的函数。如果数据集中可能包含非数值数据，请使用STDEVA函数；否则，请使用STDEV函数。

四、标准差的应用

标准差在数据分析、统计学和质量控制等领域有着广泛的应用。以下是一些常见的应用场景：

1. 质量控制：在制造业中，标准差用于评估生产过程的稳定性。通过计算产品质量的标准差，可以判断生产过程是否存在异常波动，从而采取相应的改进措施。

2. 投资决策：在金融领域，标准差用于衡量投资组合的风险。标准差越大，说明投资组合的波动越大，风险越高；标准差越小，说明投资组合越稳定，风险越低。

3. 市场研究：在市场研究中，标准差用于分析消费者行为的差异。通过计算不同消费者群体的标准差，可以了解各群体之间的差异程度，从而制定更具针对性的营销策略。

4. 学术研究：在学术研究中，标准差用于衡量实验数据的离散程度。通过比较不同实验组的标准差，可以判断实验结果的稳定性和可靠性。

五、总结

在Excel中计算标准差是一个简单而重要的任务。通过使用STDEV和STDEVA等函数，我们可以轻松地计算数据集的标准差，从而了解数据的离散程度。在实际应用中，我们需要注意数据类型的一致性、样本与总体的区别、空单元格的处理以及数据的代表性等问题。通过合理选择和使用这些函数，我们可以更好地分析和利用数据集中的信息。