揭秘:AXA的数值究竟是多少?
在数学的世界中,表达式“a×a”或者简写为“a²”(读作“a的平方”)是一个基础且频繁出现的概念。当我们问“axa等于多少呀”,实际上是在探讨一个数的平方值是多少,这个问题看似简单,实则蕴含着丰富的数学意义和应用。本文将带你深入了解平方的概念、性质、计算方法以及在实际生活中的应用,旨在帮助读者全面理解“axa等于多少呀”这一数学问题的本质。
一、平方的定义
平方,简单来说,就是一个数自乘的结果。对于任意实数a,它的平方表示为a²,即a×a。例如,5的平方(5²)就是5×5=25;-3的平方(-3²)则是(-3)×(-3)=9。平方运算是一种基本的代数运算,它不仅在数学内部扮演着重要角色,也是物理学、工程学、经济学等多个学科领域的基础工具。

二、平方的性质
1. 非负性:对于所有实数a,其平方a²总是非负的。这是因为任何实数乘以自己都是非负的。特别地,当a=0时,a²=0,是平方运算中的唯一零点。
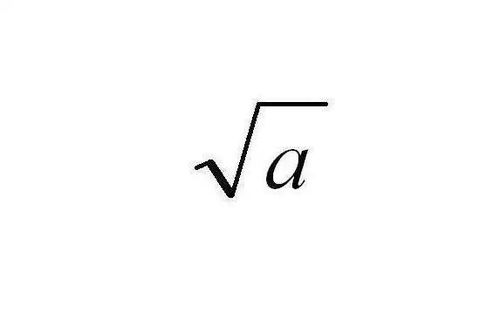
2. 对称性:对于任意实数a,其平方a²等于其相反数-a的平方,即a²=(-a)²。这意味着平方运算具有关于原点对称的性质。

3. 递增性:在实数范围内,随着a的绝对值增大,a²的值也随之增大。这表明平方函数在正数区间和负数区间上都是单调递增的(忽略负号影响)。
4. 乘法性质:对于任意实数a和b,(ab)²=a²b²。这是乘法分配律在平方运算中的体现,也是解决复杂平方问题的重要工具。
三、平方的计算方法
计算一个数的平方,最直接的方法就是将这个数自乘。然而,对于较大的数或需要频繁计算的场景,掌握一些技巧和方法可以大大提高效率。
1. 直接计算:对于较小的数,直接相乘是最简单的方法。例如,计算4的平方,直接得出4×4=16。
2. 利用平方表:在学习初期,可以制作或使用平方表来快速查找常用数的平方值。
3. 分解法:对于较大的数,可以尝试将其分解为两个较小数的乘积,然后分别求这两个数的平方,再利用乘法性质得出结果。例如,计算32的平方,可以看作(4×8)²=4²×8²=16×64=1024。
4. 近似估算:对于非整数或需要快速估算的情况,可以利用一些数学技巧进行近似计算。比如,利用平方根的性质,如果知道一个数的平方根,可以平方这个根来得到原数的平方。
四、平方在实际生活中的应用
平方不仅在纯数学领域有着广泛的应用,在日常生活和工作中也无处不在,以下是一些具体实例:
1. 面积计算:在几何学中,平方是计算平面图形面积的基础。例如,正方形的面积等于边长的平方;圆形的面积可以通过半径的平方与π的乘积来计算。
2. 物理学中的能量与力:在物理学中,平方经常出现在描述能量、力、速度等物理量的公式中。例如,动能公式E=1/2mv²表明物体的动能与其质量的平方和速度的平方成正比。
3. 经济学中的增长与收益:在经济学中,平方常用于表示增长率、收益率等指标的平方关系。例如,复利计算公式中,本金在t年后的增长额与利率的平方和时间的乘积有关。
4. 工程学中的应力与强度:在工程学中,材料的应力、强度等参数的计算往往涉及到平方运算。例如,梁的弯曲应力与其横截面积的平方成反比。
5. 统计学中的方差:在统计学中,方差是衡量数据集离散程度的重要指标,其计算公式中包含了数据点与均值之差的平方和。
五、平方与数学思维的培养
学习平方不仅是为了掌握一种数学运算,更重要的是通过这一过程培养数学思维和解决问题的能力。平方运算背后的逻辑、性质以及在实际中的应用,都是锻炼逻辑思维、抽象思维和解决实际问题能力的绝佳素材。
1. 逻辑思维:通过理解平方的定义和性质,可以培养严谨的逻辑思维和推理能力。
2. 抽象思维:平方运算将具体的数值运算抽象为代数表达式的形式,有助于提升抽象思维能力。
3. 问题解决:在实际应用中,遇到需要用到平方运算的问题时,能够灵活运用所学知识,设计合理的解决方案。
六、结语
综上所述,“axa等于多少呀”这一看似简单的问题,实则蕴含着丰富的数学知识和广泛的应用价值。通过对平方概念的深入理解、性质的全面把握以及计算方法的熟练掌握,我们不仅能够轻松应对数学考试中的相关题目,更能在日常生活和工作中运用所学知识解决实际问题。因此,无论是对于数学学习还是个人能力的提升,掌握平方的相关知识都是至关重要的。希望本文能够帮助读者更好地理解和应用平方这一数学工具,从而在数学学习和实际生活中取得更大的进步和成就。
- 上一篇: 年糕的6大创意烹饪秘籍,解锁美味新体验!
- 下一篇: 幼儿园小班教具:多彩分类,开启智慧之门
-
 揭秘:第一宇宙速度的神秘数值究竟是多少?资讯攻略10-27
揭秘:第一宇宙速度的神秘数值究竟是多少?资讯攻略10-27 -
 揭秘!8K纸尺寸究竟是多少厘米?资讯攻略11-05
揭秘!8K纸尺寸究竟是多少厘米?资讯攻略11-05 -
 8开纸尺寸详解:具体厘米数值一网打尽资讯攻略10-31
8开纸尺寸详解:具体厘米数值一网打尽资讯攻略10-31 -
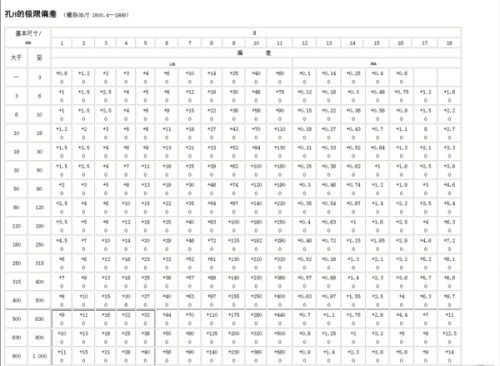 h7公差的具体数值是多少资讯攻略10-28
h7公差的具体数值是多少资讯攻略10-28 -
 揭秘:标准楼梯扶手高度的安全准则是多少?资讯攻略10-29
揭秘:标准楼梯扶手高度的安全准则是多少?资讯攻略10-29 -
 揭秘:铜的密度究竟是多少?资讯攻略11-18
揭秘:铜的密度究竟是多少?资讯攻略11-18












