如何轻松计算标准偏差
标准偏差是一种统计度量,用于量化数据集的离散程度或分散程度。简而言之,它告诉我们数据点相对于数据集的平均值(均值)有多远。标准偏差越大,表示数据点越分散;标准偏差越小,表示数据点越集中。计算标准偏差的过程可以分为几个步骤,涉及计算均值、计算每个数据点与均值的差的平方、求这些平方差的平均值,并最终取平方根。下面将从定义、计算步骤、样本标准偏差与总体标准偏差的区别、应用及实例等多个维度详细阐述如何计算标准偏差。

首先,明确标准偏差的定义。标准偏差(通常表示为σ或s)是数据集中每个数值与均值之差的平方的平均数的平方根。它反映了数据集的波动性或分散程度。标准偏差的计算公式依据是否处理的是整个数据集(总体)还是数据集的一个子集(样本)而有所不同。

计算步骤
1. 计算均值:均值是所有数据点之和除以数据点的数量。记数据集为{x1, x2, ..., xn},均值μ的计算公式为:
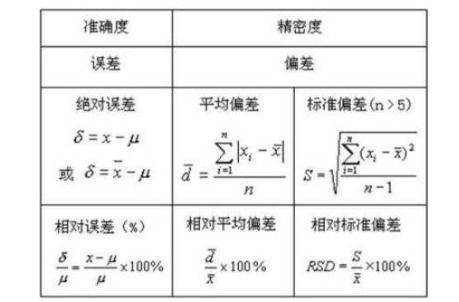
μ = (x1 + x2 + ... + xn) / n
2. 计算每个数据点与均值的差:对每个数据点xi,计算其与均值μ的差,即xi - μ。
3. 计算差的平方:将每个数据点与均值的差的平方计算出来,即(xi - μ)²。
4. 计算平方差的平均值:将所有平方差加起来,然后除以数据点的数量n(对于总体)或n-1(对于样本),得到平方差的平均值。如果处理的是样本,使用n-1作为分母是为了得到无偏估计。
5. 取平方根:将上一步得到的平均值取平方根,即得到标准偏差。
样本标准偏差与总体标准偏差的区别
在处理数据时,我们需要区分是计算总体的标准偏差还是样本的标准偏差。总体是指我们感兴趣的全部数据,而样本是从总体中随机抽取的一部分数据。
总体标准偏差:当我们有总体的全部数据时,计算标准偏差时使用n作为分母,即公式为σ = √[Σ(xi - μ)² / n]。
样本标准偏差:当我们只有总体的一部分数据时,为了得到更准确的总体标准偏差的估计,我们使用n-1作为分母,即公式为s = √[Σ(xi - μ')² / (n - 1)],其中μ'是样本均值。这种计算方法称为贝塞尔修正,它使得样本标准偏差成为总体标准偏差的无偏估计。
应用
标准偏差在统计分析、质量控制、金融、科学研究等众多领域都有广泛应用。以下是一些主要应用场景:
1. 质量控制:在制造业中,标准偏差用于监控生产过程的稳定性。如果产品的某个特性(如尺寸、重量)的标准偏差增大,可能意味着生产过程出现了波动,需要采取纠正措施。
2. 金融市场:标准偏差用于量化股票价格的波动性。高标准偏差表明价格波动大,风险高;低标准偏差表明价格波动小,风险低。
3. 科学研究:在生物学、物理学、社会学等领域,标准偏差用于衡量实验结果的离散程度,帮助科学家评估数据的可靠性和实验的有效性。
4. 统计分析:标准偏差是许多统计测试的基础,如t检验和z检验,用于比较不同数据集或判断数据点是否异常。
实例
假设我们有一个包含5个数据点的样本数据集:{4, 6, 8, 10, 12}。
1. 计算均值:
μ' = (4 + 6 + 8 + 10 + 12) / 5 = 8
2. 计算每个数据点与均值的差:
{4 - 8, 6 - 8, 8 - 8, 10 - 8, 12 - 8} = {-4, -2, 0, 2, 4}
3. 计算差的平方:
{(-4)², (-2)², 0², 2², 4²} = {16, 4, 0, 4, 16}
4. 计算平方差的平均值:
Σ(差的平方) / (n - 1) = (16 + 4 + 0 + 4 + 16) / 4 = 40 / 4 = 10
5. 取平方根:
s = √10 ≈ 3.16
因此,这个样本数据集的标准偏差约为3.16。
注意事项
数据分布:标准偏差对数据的分布形状敏感。对于正态分布的数据,标准偏差提供了良好的离散程度度量;但对于非正态分布的数据,可能需要其他统计量(如四分位距)来更好地描述数据的分散程度。
样本大小:样本大小对标准偏差的计算有重要影响。样本越大,标准偏差的估计越接近总体的真实标准偏差;样本越小,标准偏差的估计可能越不稳定。
解释标准偏差:标准偏差本身是一个绝对值,通常需要结合数据的背景进行解释。例如,在身高数据中,一个标准偏差可能代表几厘米的差异;在金融数据中,一个标准偏差可能代表百分之几的价格波动。
通过以上分析,我们可以看到标准偏差是一个简单而强大的统计工具,能够帮助我们理解和量化数据的离散程度。无论是进行质量控制、投资决策还是科学研究,掌握标准偏差的计算和应用都是非常重要的。
-
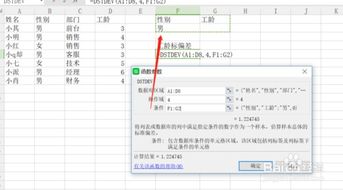 Excel中标准偏差计算的高效公式资讯攻略11-22
Excel中标准偏差计算的高效公式资讯攻略11-22 -
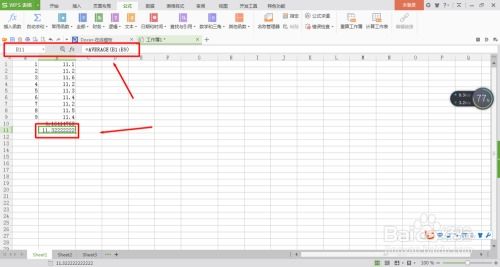 如何在Excel中计算标准偏差资讯攻略11-30
如何在Excel中计算标准偏差资讯攻略11-30 -
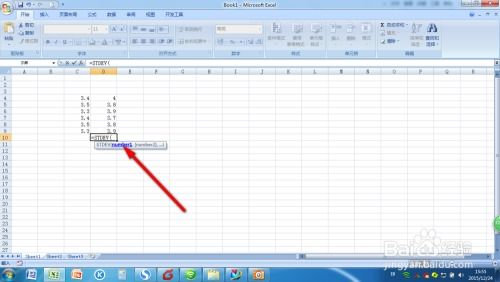
 如何在Excel中计算标准偏差的公式?资讯攻略11-22
如何在Excel中计算标准偏差的公式?资讯攻略11-22 -
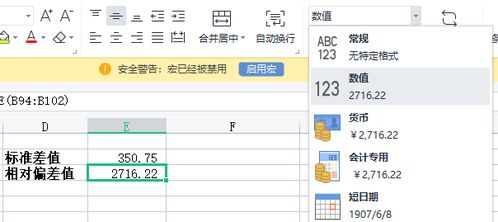
 Excel中计算相对标准偏差值的方法资讯攻略11-21
Excel中计算相对标准偏差值的方法资讯攻略11-21 -
 Excel求标准偏差的实用教程资讯攻略11-29
Excel求标准偏差的实用教程资讯攻略11-29 -
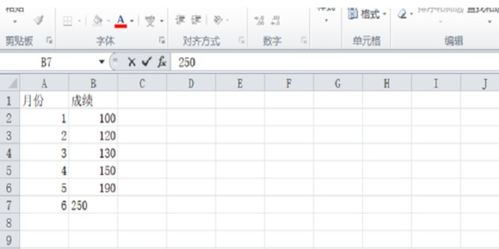 RSD%的计算方法是什么?资讯攻略12-02
RSD%的计算方法是什么?资讯攻略12-02