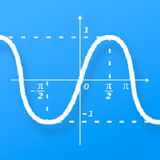
掌握指数函数！必知的8个基本公式

指数函数是数学中一个重要的概念，广泛应用于科学、工程、经济等多个领域。掌握指数函数的基本公式对于理解和应用这一概念至关重要。以下是关于指数函数八个基本公式的详细阐述。

首先，我们需要了解指数函数的基本形式：y = a^x，其中a为底数，x为指数。不同的底数和指数组合，可以产生不同的函数图像和性质。接下来，我们逐一介绍这八个基本公式。

第一个公式是指数法则的乘法公式，即a^m × a^n = a^(m+n)。这个公式表明，当底数相同时，两个指数函数相乘，其指数相加。例如，a^2 × a^3 = a^(2+3) = a^5。这个公式是指数函数运算中最基本的一个，它简化了指数函数的乘法运算。

第二个公式是指数法则的除法公式，即a^m ÷ a^n = a^(m-n)。这个公式表明，当底数相同时，两个指数函数相除，其指数相减。例如，a^5 ÷ a^3 = a^(5-3) = a^2。这个公式同样简化了指数函数的除法运算。

第三个公式是指数法则的幂的幂公式，即(a^m)^n = a^(m×n)。这个公式表明，一个指数函数的幂的幂，等于其指数相乘。例如，(a^2)^3 = a^(2×3) = a^6。这个公式对于处理复杂的指数表达式非常有用。

第四个公式是指数法则的零指数幂公式，即a^0 = 1（a ≠ 0）。这个公式表明，任何非零数的零次幂都等于1。这是指数函数中的一个重要特性，它简化了包含零次幂的指数表达式。

第五个公式是指数法则的负指数幂公式，即a^(-m) = 1/a^m（a ≠ 0）。这个公式表明，一个数的负次幂等于其倒数的正次幂。例如，a^(-2) = 1/a^2。这个公式扩展了指数函数的定义域，使得我们可以处理包含负指数的表达式。

第六个公式是指数函数的增长性质，即当a > 1时，函数y = a^x随着x的增大而增大；当0 < a < 1时，函数y = a^x随着x的增大而减小。这个性质揭示了指数函数在不同底数下的增长或衰减趋势。对于大于1的底数，指数函数呈现爆炸式增长；而对于小于1但大于0的底数，指数函数则呈现逐渐减小的趋势。

第七个公式是自然指数函数e^x的性质，其中e是自然对数的底数（约等于2.71828）。自然指数函数e^x具有许多重要的性质，如它是自身的导数，即(e^x)' = e^x。此外，自然指数函数在微积分、物理学和工程学等领域有着广泛的应用。

第八个公式是指数函数与对数函数的关系公式，即如果y = a^x（a > 0，a ≠ 1），那么x = log_a(y)。这个公式建立了指数函数与对数函数之间的桥梁，使得我们可以利用对数函数来求解指数方程的解。同时，这个公式也揭示了指数函数与对数函数之间的互逆关系。

以上八个公式构成了指数函数的基本框架，它们涵盖了指数函数的基本运算、性质以及与其他函数的关系。掌握这些公式对于理解和应用指数函数至关重要。

在实际应用中，我们可以利用这些公式来解决各种与指数函数相关的问题。例如，在金融学领域，我们可以利用指数函数来计算复利、折旧等；在物理学领域，我们可以利用自然指数函数来描述放射性衰变、人口增长等现象；在工程学领域，我们可以利用指数函数来描述电路中的电流、电压等参数的变化规律。

此外，这些公式还可以帮助我们理解一些更复杂的数学概念。例如，在微积分中，我们可以利用指数函数的性质来求解导数、积分等问题；在概率论中，我们可以利用指数分布来描述某些随机事件发生的时间间隔；在复变函数中，我们可以利用指数函数来描述复数的指数形式等。

总之，指数函数的八个基本公式是数学中一个重要的组成部分。它们不仅简化了指数函数的运算和性质描述，还为其他数学概念和实际问题提供了有力的工具。因此，我们应该深入学习和理解这些公式，以便更好地应用它们来解决实际问题。