探寻三角函数解析式的求解策略

探寻三角函数解析式的奥秘：多种方法一网打尽

在数学的浩瀚宇宙中，三角函数犹如璀璨星辰，引领着我们探索几何与代数的交融之美。求解三角函数的解析式，就如同解锁这些星辰背后的秘密，让我们得以窥见数学世界的无限可能。今天，就让我们一起踏上这场奇妙的旅程，探索求解三角函数解析式的几种高效方法。

一、待定系数法：寻找函数的神秘钥匙

待定系数法，如同一位侦探，通过已知的信息，逐步拼凑出函数的完整面貌。这种方法的核心在于根据题目给出的条件，设立一个包含未知系数的三角函数表达式，然后利用已知条件逐步求解这些未知系数。

例如，已知一个正弦型函数在特定点的取值和周期，我们可以设该正弦型函数为y=Asin(ωx+φ)，其中A、ω、φ为待求系数。通过代入已知条件，我们可以列出方程组，进而求解出A、ω、φ的值，从而得到函数的解析式。

这种方法的关键在于设立合理的函数表达式，并充分利用已知条件列出方程组。通过待定系数法，我们可以将复杂的三角函数问题转化为简单的代数问题，从而轻松求解。

二、图象变换法：函数图像的魔法之旅

图象变换法，则是通过观察和分析函数图像的变化规律，来求解三角函数的解析式。这种方法将抽象的数学表达式转化为直观的图像，让我们能够更清晰地看到函数的变化趋势和周期性。

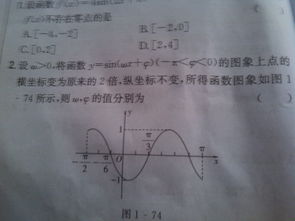
具体来说，图象变换法包括平移变换、伸缩变换、翻折变换等。例如，已知一个正弦函数的图像向左平移了π/6个单位，且振幅变为原来的2倍，我们可以根据这些信息，推断出原函数的解析式应为y=2sin(2x+π/6)。

图象变换法的优点在于直观易懂，能够让我们通过图像的变化规律来推断函数的解析式。但需要注意的是，这种方法要求我们对函数图像有深入的理解和分析能力，才能准确判断图像的变化规律。

三、方程组法：求解多元函数的利器

方程组法，则是通过列出包含多个未知数的方程组，来求解三角函数的解析式。这种方法适用于已知多个条件，且这些条件能够构成方程组的情况。

例如，已知一个余弦型函数在特定点的取值和周期，以及该函数与另一个正弦型函数的和差关系，我们可以设该余弦型函数为y=Acos(ωx+φ)，并结合已知条件列出方程组。通过求解方程组，我们可以得到A、ω、φ的值，从而得到函数的解析式。

方程组法的关键在于充分利用已知条件列出方程组，并熟练掌握求解方程组的方法。通过方程组法，我们可以将复杂的三角函数问题转化为简单的方程求解问题，从而大大提高解题效率。

四、赋值法：化简复杂问题的巧思

赋值法，则是一种通过给变量赋予特定值来化简复杂问题的巧妙方法。在求解三角函数解析式的过程中，有时我们会遇到一些难以直接求解的问题，这时就可以尝试使用赋值法来化简问题。

例如，已知一个三角函数在特定点的取值，且该函数满足某种对称关系，我们可以尝试给变量赋予满足对称关系的特定值，从而化简问题并求解出函数的解析式。

赋值法的关键在于灵活运用对称关系等性质来化简问题，并熟练掌握三角函数的基本性质和公式。通过赋值法，我们可以将复杂的三角函数问题化简为简单的代数问题或几何问题，从而轻松求解。

五、正余弦定理法：几何问题的桥梁

正余弦定理法，则是通过利用正余弦定理来求解三角函数的解析式。这种方法主要适用于涉及三角形边长和角度的问题，通过正余弦定理可以将三角形的边长和角度关系转化为三角函数关系，从而求解出函数的解析式。

例如，在已知三角形的两边长和夹角的情况下，我们可以利用余弦定理求出第三边的长度，然后利用正弦定理求出其他两个角的正弦值，进而得到三角函数的解析式。

正余弦定理法的关键在于熟练掌握正余弦定理的公式和性质，并能够灵活运用这些公式和性质来求解问题。通过正余弦定理法，我们可以将复杂的几何问题转化为简单的三角函数问题，从而大大提高解题效率。

结语：掌握方法，轻松求解

求解三角函数的解析式，既是一场对数学思维的考验，也是一次对数学美的探索。通过待定系数法、图象变换法、方程组法、赋值法以及正余弦定理法等多种方法，我们可以轻松应对各种复杂的三角函数问题。

掌握这些方法的关键在于深入理解三角函数的性质和公式，并能够灵活运用这些性质和公式来解决问题。同时，还需要注重培养自己的数学思维和解题能力，通过不断的练习和实践来提高自己的解题水平。

希望本文能够为大家提供一些有益的启示和帮助，让大家在求解三角函数解析式的道路上更加游刃有余。让我们一起在数学的世界里探索未知、追求真理、享受数学带来的乐趣吧！