揭秘三阶幻方的神奇规律
三阶幻方的规律探索
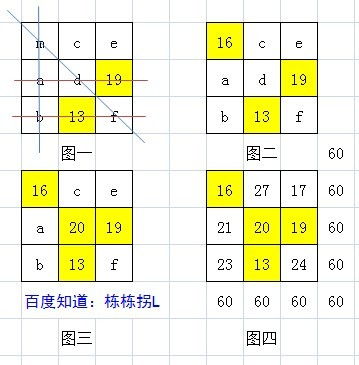
三阶幻方,又称为九宫格,是一种古老的数学游戏。其定义是将1至9这九个自然数填入一个3x3的矩阵中,使得每一行、每一列以及两条对角线上的数字之和都相等。这个相等的和被称为“幻和”。在三阶幻方中,幻和总是15。接下来,我们将深入探讨三阶幻方的各种规律和性质,帮助读者更全面地理解这一数学奇观。

一、数字唯一性与幻和
在三阶幻方中,每个数字1至9只能出现一次。这是确保幻方有效的基本条件。幻和的性质是每行、每列以及对角线上的三个数字之和等于15。这一规律是三阶幻方的核心,也是判定一个矩阵是否为幻方的依据。
二、中心数的性质
在三阶幻方中,中心数扮演着特殊角色。它不仅位于矩阵的中心位置,而且它的值等于幻和除以3,即5。换句话说,中心数是唯一能够直接通过幻和计算出来的数字。更有趣的是,中心数与过中心的三个数(中心数及其上下的两个数或左右的两个数)构成等差数列。这一性质为构造和解析幻方提供了重要的线索。
三、等差数列与中心对称
过中心线的三个数(无论是水平还是垂直)总是构成等差数列。这意味着,如果我们知道中心数和其中一个相邻数,就可以很容易地推算出另一个相邻数。此外,中心对称的两个数(即关于中心位置对称的两个数)的平均数等于中心数。这一规律帮助我们在填充幻方时保持平衡和对称。
四、边角关系与金三角法
边角关系是三阶幻方中的另一个重要规律。它指出,相邻两边(非对角线)的中间数之和等于不同边的角数乘以2。这一规律有助于我们在构造幻方时验证和调整数字的位置。此外,金三角法也是一种有效的构造方法。它基于这样一个规律:每个角数的两倍等于其对角相邻数的和。例如,在一个正确的三阶幻方中,如果角上的数是6,那么其对角相邻的两个数之和应该是12(6的两倍)。
五、构造方法与示例
构造三阶幻方的方法有多种,包括Siamese方法、罗伯特法等。这里我们介绍一种常用的构造方法:
1. 将1放在第一行的中间位置。
2. 下一个数字放在其右上方(如果超出矩阵边界,则回到第一行)。
3. 如果右上方已经有数字或超出矩阵边界,则放在其正下方。
4. 重复步骤2和3,直到所有数字都被填入。
以这种方法,我们可以得到一个正确的三阶幻方:
```
8 1 6
3 5 7
4 9 2
```
在这个幻方中,每一行、每一列以及两条对角线上的数字之和都是15。
六、幻方的文化意义与应用
三阶幻方不仅在数学上具有趣味性,而且在文化和宗教中扮演着重要角色。相传,大禹治水时,洛水中出现了一个“神龟”,背上有美妙的图案,史称“洛书”。用数字翻译出来,就是三阶幻方。古印度与古阿拉伯人也广泛传播和使用三阶幻方,认为它可以辟邪驱疫。人们甚至将刻着三阶幻方的金属片挂在脖子上作为护身符。
在西周时期,三阶幻方(洛书)与伏羲八卦相融合,演变为文王八卦。文王八卦主要用于三元九运、玄空风水等方面。三元九运主要预测天运,玄空风水主要预测地运,而八字算命则主要预测人运。三阶幻方的九个数字与六十甲子相结合,形成了180年为一个周期的三元九运理论。
在现代社会中,三阶幻方的应用也日益广泛。例如,在计算机科学中,幻方被用于数据加密和图像处理等领域。其独特的结构和性质使得它在这些领域具有独特的优势。
七、高级规律与线性表示
除了上述基本规律外,三阶幻方还具有一些高级规律和性质。例如,与每个角顶数相邻的两数之和等于对角顶的数的二倍。这一规律进一步增强了幻方的对称性和平衡性。
此外,三阶幻方还具有线性叠加性。两个三阶幻方的对应元素相加,仍然得到一个三阶幻方。用一个数去乘三阶幻方的每个元素,也能得到一个新的三阶幻方。这些性质为幻方的扩展和变形提供了可能。
在更深的数学层面上,三阶幻方的元素之间存在确定的线性关系。这意味着,我们仅通过某三个元素就可以完全表示出三阶幻方的其他元素。这一性质不仅在数学理论上具有重要意义,而且在幻方的构造和解析中也具有实际应用价值。
八、总结
三阶幻方是一种古老而有趣的数学游戏,它以其独特的结构和性质吸引了无数数学爱好者和研究者。通过本文的介绍,我们了解了三阶幻方的基本规律、中心数的性质、等差数列与中心对称、边角关系与金三角法、构造方法与示例、文化意义与应用以及高级规律与线性表示等方面的知识。这些知识不仅有助于我们更好地理解和欣赏三阶幻方,而且为我们探索更复杂的数学问题和解决实际问题提供了有益的启示。
三阶幻方不仅展示了数学的美妙和神奇,而且反映了人类对自然界的深刻洞察和理性思考。通过学习和研究三阶幻方,我们可以更好地领略数学的魅力,激发对科学的兴趣和热情。
- 上一篇: WPS中创建表格的步骤
- 下一篇: 如何在叨叨记账中修改角色设置
-
 揭秘!凸透镜成像规律的神奇口诀与深度解析资讯攻略11-27
揭秘!凸透镜成像规律的神奇口诀与深度解析资讯攻略11-27 -
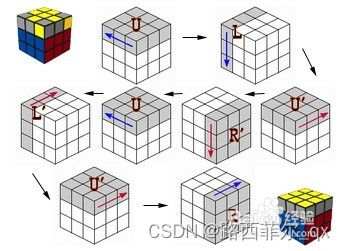 三阶魔方教程怎么学?资讯攻略11-21
三阶魔方教程怎么学?资讯攻略11-21 -
 三阶魔方图解教程:白话版·手把手速成指南资讯攻略11-08
三阶魔方图解教程:白话版·手把手速成指南资讯攻略11-08 -
 【速成攻略】揭秘三阶魔方第三层终极解法,图解让你轻松掌握!资讯攻略11-07
【速成攻略】揭秘三阶魔方第三层终极解法,图解让你轻松掌握!资讯攻略11-07 -
 解锁三阶魔方终极层:第三层公式口诀大揭秘!资讯攻略11-10
解锁三阶魔方终极层:第三层公式口诀大揭秘!资讯攻略11-10 -
 三阶魔方还原教程(三步速成)资讯攻略11-09
三阶魔方还原教程(三步速成)资讯攻略11-09












