奇偶函数相加，结果竟是？奇+奇、偶+偶、奇+偶分别得到什么函数？

在数学的奇妙世界里，函数如同一座座形态各异的桥梁，连接着未知与已知。而在这些桥梁中，奇函数和偶函数以其独特的对称性吸引着无数数学爱好者的目光。当我们把奇函数和偶函数进行加减运算时，会碰撞出怎样的火花呢？本文将带您一探究竟，深入了解奇函数加偶函数、奇函数加奇函数、偶函数加偶函数分别会得到什么类型的函数。

奇函数与偶函数的定义

首先，让我们来回顾一下奇函数和偶函数的定义。

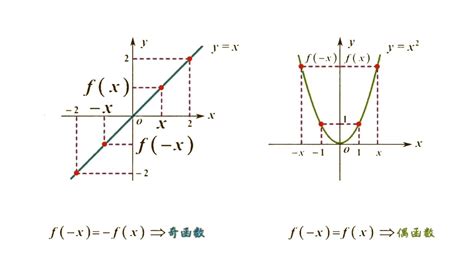
奇函数：如果对于函数f(x)，满足f(-x)=-f(x)，则称f(x)为奇函数。奇函数的图像关于原点对称。

偶函数：如果对于函数g(x)，满足g(-x)=g(x)，则称g(x)为偶函数。偶函数的图像关于y轴对称。

有了这个基础，我们就可以开始探讨奇函数与偶函数相加后的结果了。

奇函数加偶函数：非奇非偶函数

想象一下，我们手中有一个奇函数和一个偶函数，就像两幅对称图案的拼图。当我们将它们拼在一起时，得到的图案可能既不会像奇函数那样关于原点对称，也不会像偶函数那样关于y轴对称。

具体来说，设f(x)为奇函数，g(x)为偶函数，则它们的和F(x)=f(x)+g(x)满足：

F(-x)=f(-x)+g(-x)=-f(x)+g(x)

由于F(-x)既不等于F(x)（不满足偶函数的定义），也不等于-F(x)（不满足奇函数的定义），因此F(x)既不是奇函数也不是偶函数。我们称这类函数为非奇非偶函数。

举个例子，设f(x)=x（奇函数）和g(x)=x^2（偶函数），则它们的和F(x)=x+x^2就是一个非奇非偶函数。

奇函数加奇函数：奇函数

接下来，我们来看看两个奇函数相加的结果。就像两个完全相同的拼图碎片拼在一起，得到的图案仍然保持着原有的对称性。

设f(x)和h(x)都是奇函数，则它们的和F(x)=f(x)+h(x)满足：

F(-x)=f(-x)+h(-x)=-f(x)-h(x)=-F(x)

由于F(-x)=-F(x)，满足奇函数的定义，因此F(x)仍然是奇函数。

举个例子，设f(x)=x和h(x)=3x（都是奇函数），则它们的和F(x)=x+3x=4x仍然是一个奇函数。

偶函数加偶函数：偶函数

与奇函数相加类似，两个偶函数相加也会保持原有的对称性，但这次是关于y轴的。

设g(x)和m(x)都是偶函数，则它们的和G(x)=g(x)+m(x)满足：

G(-x)=g(-x)+m(-x)=g(x)+m(x)=G(x)

由于G(-x)=G(x)，满足偶函数的定义，因此G(x)仍然是偶函数。

举个例子，设g(x)=x^2和m(x)=4x^2（都是偶函数），则它们的和G(x)=x^2+4x^2=5x^2仍然是一个偶函数。

深入探索：函数加减运算的对称性

通过上述例子，我们可以发现奇函数和偶函数在加减运算中的对称性有着有趣的规律。这背后其实隐藏着更深层次的数学原理。

对称性原理：奇函数和偶函数的定义本身就是基于对称性的。奇函数关于原点对称，偶函数关于y轴对称。当我们将两个具有相同对称性的函数相加时，得到的函数仍然会保持这种对称性。而当我们将一个奇函数和一个偶函数相加时，由于它们的对称性不同，得到的函数将不再保持原有的对称性。

线性运算性质：函数的加减运算属于线性运算。线性运算不会改变函数的奇偶性（当且仅当两个函数具有相同的奇偶性时）。这意味着，如果我们有两个奇函数或两个偶函数进行加减运算，结果仍然会保持原有的奇偶性。但当我们混合使用奇函数和偶函数时，结果将不再具有明确的奇偶性。

应用与实践：函数性质的灵活运用

了解奇函数和偶函数在加减运算中的性质不仅有助于我们更好地理解函数的本质，还可以在实际问题中灵活运用这些性质来解决问题。

例如，在信号处理领域，奇函数和偶函数常用于描述信号的对称性。通过分析信号的奇偶性，我们可以更好地理解信号的性质并进行相应的处理。此外，在微积分和微分方程等领域中，奇函数和偶函数的性质也经常被用于求解问题和简化计算。

结语

奇函数加偶函数、奇函数加奇函数、偶函数加偶函数分别会得到什么类型的函数？通过本文的详细探讨，我们得出了以下结论：奇函数加偶函数得到的是非奇非偶函数；奇函数加奇函数得到的是奇函数；偶函数加偶函数得到的是偶函数。这些结论不仅有助于我们深入理解函数的奇偶性及其运算规律，还可以在实际问题中灵活运用这些性质来解决问题。

在数学的世界里，奇函数和偶函数就像两颗璀璨的明珠，它们以其独特的对称性和运算规律吸引着无数数学爱好者的目光。通过不断探索和学习，我们可以更好地掌握这些规律并运用到实际问题中去。希望本文能够为您打开一扇通往数学奇妙世界的大门！