揭秘黄金比例的神奇计算方法

在探讨如何计算黄金比例这一古老而迷人的数学概念时，我们首先要明确，黄金比例，又称黄金分割或神圣比例，是一个在自然界、艺术、建筑等领域广泛存在的数学常数。其独特的属性在于，当一个整体被分割为两部分时，这两部分的比值等于整体与较长部分的比值，这一比值通常表示为φ（phi），其近似值约为1.618。黄金比例的应用不仅增添了物体的美感，还深刻影响了人类文明的多个方面。

黄金比例的起源可以追溯到古希腊时期，毕达哥拉斯学派对其进行了深入研究。他们发现，黄金比例无处不在，无论是自然界的贝壳、植物的叶片排列，还是人类身体的比例，都隐含着这一神秘的常数。在艺术领域，黄金比例的运用更是达到了巅峰，无论是古希腊神庙的建筑设计，还是文艺复兴时期的绘画和雕塑，黄金比例都成为了艺术家们追求美的标准。

那么，如何计算黄金比例呢？有几种常见的方法可以帮助我们理解和应用这一比例。

第一种方法是使用数学公式进行计算。黄金比例的数学表达式为：a/b = (a+b)/a，其中a和b代表整体被分割成的两部分。如果我们设较长的部分为a，较短的部分为b，那么黄金比例φ就等于a/b。通过代数变换，我们可以得到φ的二次方程：φ^2 - φ - 1 = 0。解这个方程，我们得到两个解，一个正数解和一个负数解。由于在实际应用中，我们关心的是长度或比例，因此只取正数解，即φ ≈ 1.618。这个值就是我们通常所说的黄金比例。

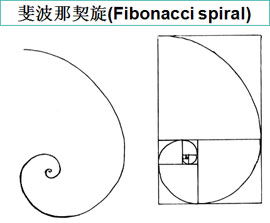
第二种方法是利用几何图形来直观展示黄金比例。最常见的是黄金矩形，其长边与短边的比值等于整体矩形的长边与较长一边的比值。如果我们从一个正方形开始，通过不断截取与正方形一边等长的部分，并在剩余部分继续画正方形，以此类推，我们会发现这一系列正方形和剩余部分的组合形成了一个黄金矩形序列。这个序列中的每个矩形都保持了黄金比例，展现出一种和谐而美丽的视觉效果。

第三种方法是使用斐波那契数列来计算黄金比例。斐波那契数列是一个从0和1开始的数列，之后的每个数字都是前两个数字的和。即：0, 1, 1, 2, 3, 5, 8, 13, ...。这个数列与黄金比例有着密切的关系。随着数列的延伸，相邻两项的比值越来越接近黄金比例φ。例如，5/3 ≈ 1.667，8/5 ≈ 1.6，13/8 ≈ 1.625，这些比值都逐渐逼近φ的近似值1.618。因此，通过计算斐波那契数列中相邻两项的比值，我们可以近似地得到黄金比例。

在实际应用中，黄金比例的计算方法可以根据具体需求进行调整。例如，在建筑设计中，设计师可能会使用黄金矩形来确定房间的比例，以营造出和谐而舒适的空间感。在艺术创作中，艺术家可能会根据黄金比例来调整人物的面部特征或身体比例，使作品更加符合人类的审美标准。此外，在金融投资、市场分析等领域，黄金比例也被用作一种分析工具，以预测市场趋势和价格波动。

值得注意的是，虽然黄金比例在许多领域都展现出了其独特的魅力，但它并非完美的解决方案。在实际应用中，我们需要根据具体情况综合考虑各种因素，以找到最适合的比例或方案。例如，在建筑设计中，除了考虑黄金比例外，还需要考虑建筑的功能性、结构安全性以及环境适应性等因素。

此外，随着科技的发展，计算机和数学软件为我们提供了更便捷的计算和分析工具。通过使用这些工具，我们可以更精确地计算黄金比例，并将其应用于更广泛的领域。例如，在计算机图形学中，黄金比例被用于生成更自然和美观的图形和动画；在数据分析和机器学习中，黄金比例也被用作一种特征选择或模型优化的方法。

总之，黄金比例作为一种古老而神秘的数学概念，在自然界、艺术、建筑等领域都展现出了其独特的魅力。通过了解和学习黄金比例的计算方法，我们可以更好地欣赏和应用这一常数，为我们的生活和工作增添更多的美感和效率。无论是通过数学公式、几何图形还是斐波那契数列来计算黄金比例，我们都可以发现这一常数背后隐藏的奥秘和美感。因此，让我们在未来的探索中继续深入研究和应用黄金比例，共同创造一个更加美好的世界。