MATLAB轻松解方程指南
怎么用MATLAB解方程

MATLAB(Matrix Laboratory)作为一种高性能的语言和环境,专门用于技术计算。其强大的数值计算能力、灵活的函数和数据结构以及易用的绘图功能,使其成为解决数学问题的首选工具之一。在解决方程问题时,MATLAB提供了多种方法和函数,可以应对从简单的一元一次方程到复杂的非线性方程组等多种情况。本文将详细介绍如何使用MATLAB来解方程,包括代数方程、微分方程以及方程组等不同维度的内容。
一、解代数方程
代数方程是最基本的一类方程,MATLAB提供了`solve`函数来求解符号形式的代数方程。
1. 解一元一次方程
对于简单的一元一次方程,例如`3x + 5 = 14`,可以直接使用`solve`函数求解。
```matlab
syms x
eq = 3*x + 5 == 14;
sol = solve(eq, x);
disp(sol);
```
执行上述代码后,MATLAB将输出方程的解`x = 3`。
2. 解一元二次方程
对于一元二次方程,例如`x^2 - 4x + 4 = 0`,同样可以使用`solve`函数。
```matlab
syms x
eq = x^2 - 4*x + 4 == 0;
sol = solve(eq, x);
disp(sol);
```
MATLAB将输出方程的解`x = [2, 2]`,表示这是一个重根。
3. 解多元一次方程组
对于多元一次方程组,例如`2x + 3y = 8`和`3x - y = 7`,可以通过传递一个方程数组给`solve`函数来求解。
```matlab
syms x y
eq1 = 2*x + 3*y == 8;
eq2 = 3*x - y == 7;
sol = solve([eq1, eq2], [x, y]);
disp(sol);
```
MATLAB将输出方程组的解`x = 3`和`y = -2/3`。
二、解微分方程
微分方程在物理学、工程学等领域有着广泛的应用,MATLAB提供了`dsolve`函数来求解符号形式的微分方程。
1. 解一阶常微分方程
对于一阶常微分方程,例如`dy/dx = x^2`,其中`y(0) = 1`,可以使用`dsolve`函数求解。
```matlab
syms y(x)
eq = diff(y, x) == x^2;
cond = y(0) == 1;
sol = dsolve(eq, cond);
disp(sol);
```
MATLAB将输出方程的解`y(x) = (1/3)*x^3 + 1`。
2. 解高阶常微分方程
对于高阶常微分方程,例如`d^2y/dx^2 - y = 0`,其中`y(0) = 1`且`dy/dx|_(x=0) = 0`,同样可以使用`dsolve`函数。
```matlab
syms y(x)
eq = diff(y, x, 2) - y == 0;
cond1 = y(0) == 1;
cond2 = diff(y, x) |_(x == 0) == 0;
sol = dsolve(eq, [cond1, cond2]);
disp(sol);
```
MATLAB将输出方程的解`y(x) = cos(x) + sin(x)`(或者等价形式)。
3. 解偏微分方程
对于偏微分方程,MATLAB通常需要结合PDE工具箱进行数值求解,但也可以通过符号计算的方法求解某些特定类型的偏微分方程。
三、解非线性方程
非线性方程比线性方程更复杂,有时无法直接求解,但MATLAB提供了多种数值方法来逼近方程的解。
1. 使用fsolve求解非线性代数方程
`fsolve`函数是MATLAB中用于求解非线性方程组的函数,它基于数值方法,如牛顿-拉夫森法。
```matlab
fun = @(x) x^2 - exp(x); % 定义方程
x0 = 0.5; % 初始猜测值
sol = fsolve(fun, x0);
disp(sol);
```
上述代码将求解方程`x^2 - exp(x) = 0`,并输出一个近似解。
2. 使用fzero求解非线性代数方程的单根
`fzero`函数用于找到单变量非线性函数的零点,它基于一种高效的搜索算法。
```matlab
fun = @(x) x^3 - x - 2; % 定义方程
x0 = 1.5; % 初始猜测值
sol = fzero(fun, x0);
disp(sol);
```
上述代码将求解方程`x^3 - x - 2 = 0`,并输出一个零点。
四、解方程组
对于包含多个方程的方程组,MATLAB同样提供了多种求解方法。
1. 使用solve求解符号方程组
对于符号方程组,可以直接使用`solve`函数,如之前提到的多元一次方程组。
2. 使用数值方法求解非线性方程组
对于非线性方程组,可以使用`fsolve`函数进行数值求解。
```matlab
fun = @(x) [x(1)^2 + x(2)^2 - 4; (x(1) - 1)^2 + x(2)^2 - 4]; % 定义方程组
x0 = [2; 0]; % 初始猜测值
sol = fsolve(fun, x0);
disp(sol);
```
上述代码将求解方程组`x^2 + y^2 = 4`和`(x - 1)^2 + y^2 = 4`,并输出一个近似解。
五、总结
MATLAB作为一种强大的数学计算工具,提供了丰富的函数和方法来求解各种类型的方程。从简单的代数方程到复杂的非线性方程组,从常微分方程到偏微分方程,MATLAB都能提供有效的解决方案。通过掌握MATLAB的基本功能和高级技巧,用户可以更加高效地解决数学和工程问题。无论是学术研究还是工程应用,MATLAB都将成为用户不可或缺的工具之一。
- 上一篇: 纸叠小船手工的折叠方法是什么?
- 下一篇: 手机上如何快速查询小客车摇号结果?
-
 Matlab方程求解资讯攻略12-06
Matlab方程求解资讯攻略12-06 -
 MATLAB安装指南资讯攻略11-14
MATLAB安装指南资讯攻略11-14 -
 Matlab Coder 应用指南资讯攻略12-05
Matlab Coder 应用指南资讯攻略12-05 -
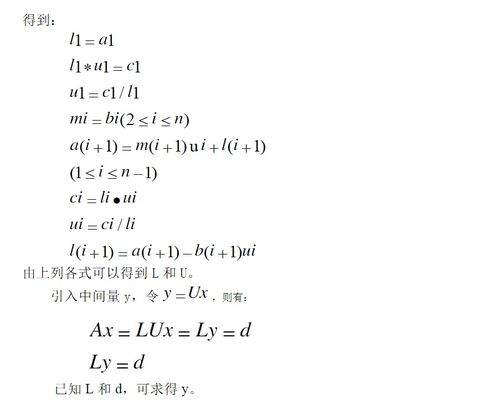 如何掌握解方程组的三种基本方法?资讯攻略11-18
如何掌握解方程组的三种基本方法?资讯攻略11-18 -
 揭秘二阶微分方程的3大通解公式!资讯攻略11-21
揭秘二阶微分方程的3大通解公式!资讯攻略11-21 -
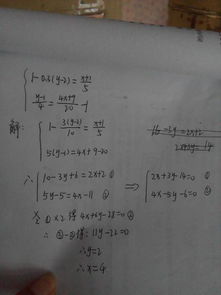 轻松掌握:方程组解法大全资讯攻略11-25
轻松掌握:方程组解法大全资讯攻略11-25