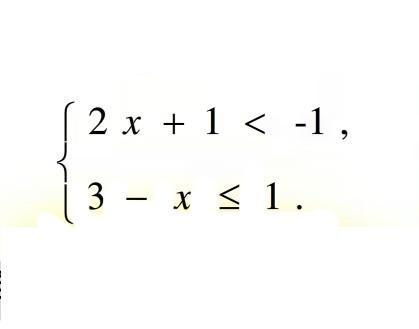深入解析Jensen不等式
Jensen不等式是什么

Jensen不等式是数学领域中凸函数理论的一个重要结果,它揭示了凸函数与随机变量期望值之间的关系。这一不等式不仅在数学理论中具有重要地位,还在经济学、金融学、机器学习等多个实际领域发挥着重要作用。本文将从多个维度探讨Jensen不等式的定义、性质、证明方法以及实际应用。

一、Jensen不等式的定义与性质
Jensen不等式描述的是凸函数与随机变量期望值之间的关系。具体来说,对于一个凸函数f和一个随机变量X,如果X的期望值E[X]存在,那么有f(E[X])≤E[f(X)]。这一不等式由丹麦数学家Johan Jensen于1906年提出,因此得名Jensen不等式。
在数学上,凸函数是指在其定义域内的任意两点间,函数的割线位于函数图像上方的函数。换句话说,对于定义在区间I上的函数f,若对I上任意的两点x1和x2,以及任意实数λ∈(0,1),总有f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),则称f为定义在I上的凸函数。相反,凹函数则是指在其定义域内的任意两点间,函数的割线位于函数图像下方的函数,其不等式方向相反。
Jensen不等式不仅适用于离散情况,也适用于连续情况。在离散情况下,X可以取有限个值,每个值对应一个概率;在连续情况下,X的取值范围是一个连续区间,对应一个概率密度函数。Jensen不等式在两种情况下都成立。
二、Jensen不等式的数学表达式与证明
Jensen不等式的数学表达式为f(E[X])≤E[f(X)],其中f表示凸函数,X表示随机变量,E[X]表示X的期望值,E[f(X)]表示f(X)的期望值。
Jensen不等式的证明方法主要基于凸函数的定义和数学归纳法。以下是一个简化的证明过程:
设f为凸函数,X为随机变量,λi为非负实数且满足∑λi=1,xi为任意实数。则有:
f(∑iλixi)≤∑iλif(xi)
这是因为f是凸函数,所以对于任意两点xi和xj以及任意实数λ∈(0,1),都有:
f(λxi+(1-λ)xj)≤λf(xi)+(1-λ)f(xj)
将上述不等式推广到n个点,即可得到:
f(∑iλixi)≤∑iλif(xi)
现在,考虑随机变量X的期望值E[X],它可以看作是X所有可能取值xi与其对应概率λi的加权和。因此,可以将E[X]代入上述不等式,得到:
f(E[X])=f(∑iλixi)≤∑iλif(xi)=E[f(X)]
这就证明了Jensen不等式。
三、Jensen不等式的常见形式与特例
Jensen不等式在特定函数形式下具有一些常见的特例和形式。以下是一些常见的凸函数形式下的Jensen不等式:
1. 幂函数:对于幂函数f(x)=xn(n≥1),Jensen不等式表示(E[X])n≤E[Xn]。
2. 对数函数:对于对数函数f(x)=ln(x)(x>0),Jensen不等式表示ln(E[X])≤E[ln(X)]。
3. 指数函数:对于指数函数f(x)=ex,虽然ex不是凸函数,但-ex是凹函数,因此可以应用Jensen不等式的反向形式,即E[ex]≥e(E[X])。
4. 三角函数:对于某些三角函数,如f(x)=cos(x)在特定区间内是凸函数或凹函数,因此也可以应用Jensen不等式。
此外,Jensen不等式还有连续形式下的推广。对于连续随机变量X和凸函数f,如果X的概率密度函数为p(x),则Jensen不等式可以表示为:
f(∫xp(x)dx)≤∫f(x)p(x)dx
其中,∫xp(x)dx表示X的期望值E[X],∫f(x)p(x)dx表示f(X)的期望值E[f(X)]。
四、Jensen不等式的实际应用
Jensen不等式在实际应用中具有广泛的应用案例,涉及经济学、金融学、机器学习等多个领域。
1. 经济学:在经济学中,可以利用Jensen不等式来分析市场均衡和资源配置问题。例如,在消费者选择理论中,可以通过Jensen不等式来推导消费者的最优消费组合。
2. 金融学:在金融学中,Jensen不等式被广泛应用于投资组合的风险和收益评估。例如,可以通过Jensen不等式来比较不同投资组合的期望收益和风险水平,从而选择最优的投资策略。
3. 机器学习:在机器学习中,Jensen不等式被用于推导算法的性能上界。例如,在支持向量机(SVM)中,可以通过Jensen不等式来估计分类器的泛化误差。
此外,Jensen不等式还与Holder不等式、Minkowski不等式等其他数学不等式之间存在一定的关联。这些不等式在数学分析中都有广泛的应用,它们之间的关联有助于更深入地理解不等式的性质和应用。
五、总结
Jensen不等式是凸函数理论中的一个重要结果,它揭示了凸函数与随机变量期望值之间的关系。通过这一不等式,我们可以对随机变量的函数值进行期望运算,并得出一些有用的结论。Jensen不等式在数学理论中具有重要的地位,同时也在经济学、金融学、机器学习等多个实际领域发挥着重要作用。
在实际应用中,我们可以根据具体问题的需求,选择合适的凸函数形式,并利用Jensen不等式来求解问题。通过不断学习和实践,我们可以更好地掌握和应用Jensen不等式,为解决实际问题提供有力的数学工具。
- 上一篇: 让掉色裤子重现原色的神奇方法
- 下一篇: 如何区分亲电取代与亲核取代?
-
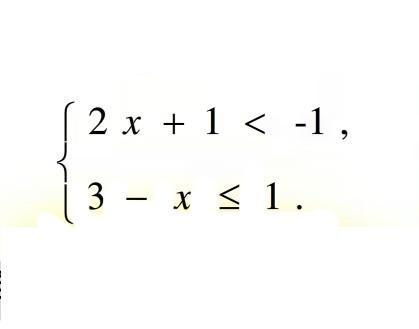 精选二十道一元一次不等式组练习资讯攻略10-31
精选二十道一元一次不等式组练习资讯攻略10-31 -
 如何在Word文档中插入不等号?资讯攻略11-22
如何在Word文档中插入不等号?资讯攻略11-22 -
 独家揭秘!比特人生新手礼包一键领取攻略 & 最新礼包码大放送,速领不等!资讯攻略11-08
独家揭秘!比特人生新手礼包一键领取攻略 & 最新礼包码大放送,速领不等!资讯攻略11-08 -
 揭秘“skirt”这个英文单词的真正含义资讯攻略11-14
揭秘“skirt”这个英文单词的真正含义资讯攻略11-14 -
 如何进行因式分解?资讯攻略11-17
如何进行因式分解?资讯攻略11-17 -
 楼顶防水补漏费用全解析:如何合理收费?资讯攻略11-21
楼顶防水补漏费用全解析:如何合理收费?资讯攻略11-21