如何计算正方体的表面积和单个面的面积？

在探索几何学的奇妙世界中，正方体作为一个基础而重要的三维形状，其面积与表面积的计算是学生们初识立体几何时必学的知识点。正方体，顾名思义，其六个面均为正方形，且各边长度相等，这种独特的性质使得其面积与表面积的计算既直观又富有教育意义。接下来，我们将详细阐述如何准确地计算正方体的面积（此处特指单一面的面积，因为正方体有多个面）以及整个正方体的表面积。

正方体单一面面积的计算

首先，我们要明确的是，正方体的每一个面都是一个正方形。正方形面积的计算公式是所有边长相乘，即边长的平方。设正方体的棱长为a（a为任意正实数），则正方体任一面的面积S可以表示为：

\[ S = a^2 \]

这个公式简单直接，是理解正方体面积计算的基础。例如，如果一个正方体的棱长是5厘米，那么它任一面的面积就是\(5^2 = 25\)平方厘米。

正方体表面积的计算

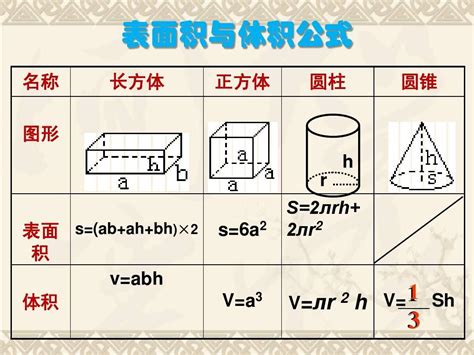
接下来，我们进一步探讨如何计算正方体的整个表面积。正方体有六个面，且每个面的面积都相等。因此，正方体表面积的计算就是将这六个面的面积相加。由于每个面的面积都是\(a^2\)，所以正方体的总表面积A可以表示为：

\[ A = 6 \times a^2 \]

这个公式体现了正方体表面积与其棱长之间的直接关系。继续以棱长为5厘米的正方体为例，其表面积\(A = 6 \times 5^2 = 6 \times 25 = 150\)平方厘米。

实践应用与深化理解

掌握了正方体面积和表面积的计算方法后，我们可以通过一些实际例子来加深理解。比如，在日常生活中，我们常见的骰子就是一个典型的正方体。如果你想要为骰子的每一个面都贴上不同颜色的贴纸，并想知道需要多少贴纸材料，那么就需要计算出骰子（即正方体）的表面积。

此外，正方体表面积的计算在建筑、工程设计等领域也有着广泛的应用。设计师们需要准确计算材料用量，以确保工程的经济性和可行性。而正方体表面积的计算公式正是这一过程中的重要工具之一。

拓展思考

除了计算正方体的面积和表面积外，我们还可以进一步思考其他相关问题。比如，如果给定一个正方体的表面积，如何求出其棱长？这需要我们逆向运用表面积的计算公式，即：

\[ a = \sqrt{\frac{A}{6}} \]

通过这个公式，我们可以快速地从给定的表面积反推出正方体的棱长。

再比如，当我们面对的是由多个正方体组成的复杂立体图形时，如何计算其总表面积？这需要我们具备将复杂图形分解为简单几何形状的能力，并灵活运用面积和表面积的计算公式进行求解。

结语

综上所述，正方体的面积和表面积计算是几何学中的基础内容，它不仅有助于我们建立对三维空间形状的基本认识，更是解决实际问题的重要工具。通过学习和掌握这些计算方法，我们可以更好地理解和应用几何学知识于日常生活和各个专业领域之中。同时，这也提醒我们，在学习任何一门学科时都应注重基础知识的掌握和灵活运用能力的培养。