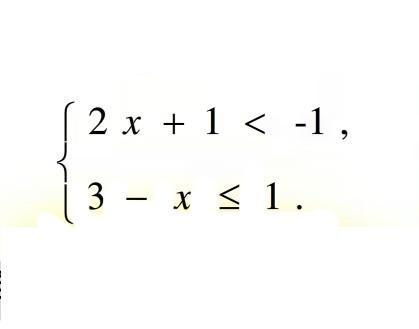一元一次方程的详细解法步骤
在数学学习中,一元一次方程是初学者接触到的最基本、也是最重要的方程类型之一。它不仅为后续的数学学习打下坚实的基础,还广泛应用于实际问题的解决中。一元一次方程是指只含有一个未知数,且未知数的最高次数为1的方程。它的一般形式为ax + b = 0(其中a ≠ 0)。本文将从理解方程概念、方程的解法步骤、特殊情况的处理、方程解的应用以及解题中的常见误区等多个维度,详细介绍如何解一元一次方程。

一、理解一元一次方程的概念
首先,我们需要明确一元一次方程的定义和构成要素。一元指的是方程中只含有一个未知数,一次指的是未知数的最高次数为1。例如,方程3x + 5 = 7就是一个典型的一元一次方程,其中x是未知数,3是x的系数,5是常数项,7也是常数,代表方程右边的值。

理解方程的概念是解题的第一步。在实际应用中,许多问题可以抽象为一元一次方程来解决,比如速度、时间、距离问题,买卖问题等。因此,掌握一元一次方程的解法,对于解决实际问题具有重要意义。

二、一元一次方程的解法步骤
解一元一次方程的基本思路是,通过移项、合并同类项、系数化为1等步骤,求出未知数的值。具体步骤如下:

1. 移项:将方程两边的常数项和未知数项分别移到同一边,使方程变为ax = c的形式。例如,对于方程3x + 5 = 7,我们可以将5移到方程的右边,得到3x = 2。
2. 合并同类项:如果方程两边有同类项(即未知数项或常数项),需要先将它们合并。但在一元一次方程中,这一步通常不是必需的,因为方程已经是最简形式。
3. 系数化为1:将未知数项的系数化为1,从而求出未知数的值。这通常通过除法来实现。例如,在方程3x = 2中,我们可以将两边同时除以3,得到x = 2/3。
三、特殊情况的处理
在解一元一次方程时,我们可能会遇到一些特殊情况,需要特殊处理:
1. 未知数系数为0:如果方程中未知数的系数为0(即a = 0),则方程变为b = c的形式,此时方程没有解,或者说方程无解,因为不存在一个未知数能满足这样的等式。
2. 方程两边相等:如果方程两边相等(即b = c),则方程变为ax = ax的形式,此时方程有无数个解,因为任何数乘以0都等于0(这里a为0,x为任意数)。但严格来说,这种情况下的方程并不符合一元一次方程的定义(因为a不能为0),所以我们通常不考虑这种特殊情况。
3. 方程中含有分数:如果方程中含有分数,为了避免分数运算的复杂性,我们通常会先将方程两边同时乘以一个适当的数(通常是分母的最小公倍数),以消去分数。例如,对于方程(1/2)x + 3 = 5,我们可以将两边同时乘以2,得到x + 6 = 10,然后再求解。
四、一元一次方程解的应用
一元一次方程的解在实际生活中有着广泛的应用。比如:
1. 速度、时间、距离问题:在行驶问题中,我们可以利用一元一次方程来计算速度、时间或距离。例如,如果一辆车以恒定速度行驶,已知行驶的总时间和总距离,就可以求出车的速度。
2. 买卖问题:在购物时,我们可能会遇到打折、满减等优惠活动。利用一元一次方程,我们可以计算出在特定条件下购买商品所需支付的总金额或获得的优惠金额。
3. 工程问题:在工程项目中,我们可以利用一元一次方程来计算完成任务所需的时间、人力或资源。例如,如果一项工作需要多人合作完成,已知每个人的工作效率和总工作量,就可以求出完成这项工作所需的总时间。
五、解题中的常见误区
在解一元一次方程时,初学者容易陷入一些误区。以下是一些常见的误区及避免方法:
1. 移项错误:在移项时,学生可能会忘记改变符号或漏掉某些项。为了避免这种错误,我们可以在移项时用铅笔轻轻划掉已移的项,并在新位置写上相应的项和符号。
2. 合并同类项时出错:在合并同类项时,学生可能会忘记加上或减去相应的项。为了避免这种错误,我们可以在合并同类项时先列出所有同类项,并仔细计算它们的和或差。
3. 系数化为1时出错:在系数化为1时,学生可能会忘记除以未知数的系数或计算出错。为了避免这种错误,我们可以在进行除法运算时先计算除数(即未知数的系数)的倒数,然后将方程
- 上一篇: 电脑与手机怎样实现连接?
- 下一篇: 揭秘:中元节具体是在哪一天?
-
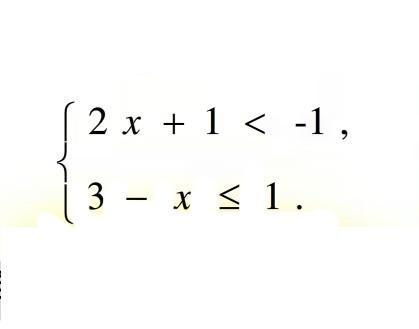 精选二十道一元一次不等式组练习资讯攻略10-31
精选二十道一元一次不等式组练习资讯攻略10-31 -
 揭秘一元二次方程公式法的绝妙解题步骤资讯攻略12-30
揭秘一元二次方程公式法的绝妙解题步骤资讯攻略12-30 -
 一元二次方程的四种求解方法资讯攻略11-11
一元二次方程的四种求解方法资讯攻略11-11 -
 探索数学奥秘:如何精准判断方程有无实数根?资讯攻略11-28
探索数学奥秘:如何精准判断方程有无实数根?资讯攻略11-28 -
 高等数学入门:全微分方程的概念及解法资讯攻略11-11
高等数学入门:全微分方程的概念及解法资讯攻略11-11 -
 轻松掌握:方程组解法大全资讯攻略11-25
轻松掌握:方程组解法大全资讯攻略11-25