双曲线的顶点坐标如何求解

在数学的世界里，双曲线以其独特的形状和性质吸引着无数探索者的目光。而当我们深入了解双曲线时，一个不可或缺的概念便是其顶点坐标。这不仅仅是一个数学上的坐标点，更是连接双曲线几何特征与代数表达式的桥梁。今天，就让我们一起揭开双曲线顶点坐标的神秘面纱，探索它背后的奥秘与魅力。

一、双曲线：几何之美与代数之妙的结合

双曲线，这个在数学领域中有着悠久历史的曲线，以其独特的双支形状和无限延伸的特性而闻名。在几何学中，它代表着一种对称与不平衡的和谐；在代数学中，它则是通过复杂的方程来精确描述的图形。无论是解析几何还是微积分，双曲线都扮演着重要的角色。

然而，当我们试图理解双曲线的性质时，一个无法绕过的关键点便是其顶点坐标。顶点坐标，这个看似简单的数学概念，实则是我们深入探究双曲线性质的起点。

二、双曲线顶点坐标：揭秘几何特征的关键

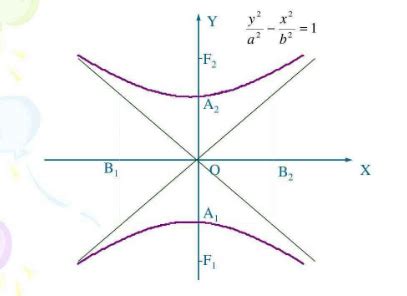
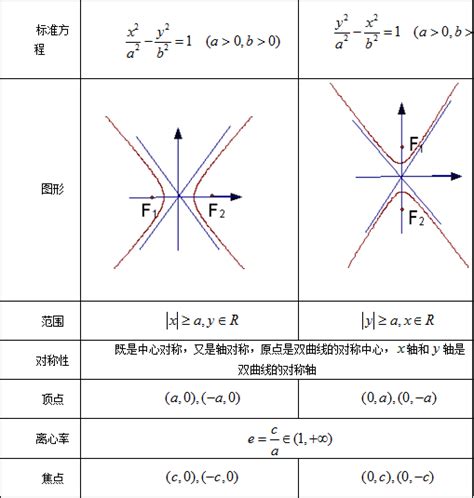
双曲线的顶点坐标，是指双曲线两支分别与x轴或y轴相交的点。在标准形式下，双曲线的顶点坐标可以通过其方程直接得出。对于形如（x^2/a^2）-（y^2/b^2）=1的双曲线（其中a、b为常数，且a>0，b>0），其顶点坐标为（±a，0）；而对于形如（y^2/a^2）-（x^2/b^2）=1的双曲线，其顶点坐标则为（0，±a）。

这些顶点坐标不仅揭示了双曲线在坐标系中的位置，还直接关联着双曲线的其他重要性质。例如，通过顶点坐标，我们可以方便地求出双曲线的焦距（即两焦点之间的距离），以及双曲线上的任意一点到两焦点的距离之差为常数这一性质。

三、深入探索：顶点坐标背后的奥秘

虽然顶点坐标在形式上看似简单，但其背后却隐藏着双曲线丰富的几何和代数性质。通过顶点坐标，我们可以更深入地理解双曲线的对称性、渐近线、离心率等关键概念。

1. 对称性：双曲线的顶点坐标揭示了其关于坐标轴的对称性。无论是关于x轴的对称还是关于y轴的对称，双曲线的顶点坐标都呈现出一种和谐与平衡。这种对称性不仅在数学上具有重要意义，还在物理学、工程学等领域中发挥着重要作用。

2. 渐近线：双曲线的渐近线是其几何特征的重要组成部分。通过顶点坐标，我们可以方便地求出双曲线的渐近线方程。这些渐近线不仅帮助我们更好地描绘双曲线的形状，还为我们研究双曲线的性质提供了有力的工具。

3. 离心率：离心率是衡量双曲线形状的一个重要参数。通过顶点坐标和焦距等参数，我们可以求出双曲线的离心率。离心率的大小直接反映了双曲线的扁平程度或陡峭程度，从而为我们提供了更直观的判断依据。

四、双曲线顶点坐标的应用：从理论到实践的跨越

双曲线顶点坐标不仅在理论研究中具有重要意义，还在实际应用中发挥着重要作用。无论是在物理学中的天体运动、光学中的光线折射，还是在工程学中的结构设计等领域，双曲线顶点坐标都扮演着不可或缺的角色。

1. 天体运动：在物理学中，双曲线轨道是行星、彗星等天体在特定条件下可能遵循的运动轨迹。通过计算双曲线的顶点坐标和其他相关参数，我们可以更准确地预测这些天体的运动轨迹和速度等关键信息。

2. 光线折射：在光学中，双曲线形状的光学元件（如双曲面镜）具有独特的折射性质。通过精确计算双曲线的顶点坐标和曲率等参数，我们可以设计出具有特定折射效果的光学元件，从而满足不同的应用需求。

3. 结构设计：在工程学中，双曲线形状的结构（如双曲线冷却塔、双曲线拱桥等）具有出色的力学性能和美学效果。通过合理设计双曲线的顶点坐标和其他相关参数，我们可以优化结构的稳定性和承载能力，同时实现美观的外观效果。

五、结语：双曲线顶点坐标——连接数学与现实的桥梁

双曲线顶点坐标，这个看似简单的数学概念，实则是连接数学理论与现实世界的桥梁。通过深入探索和理解双曲线顶点坐标的性质和应用，我们可以更好地把握数学与现实之间的联系和互动。

在数学领域中，双曲线顶点坐标不仅为我们提供了研究双曲线性质的有力工具和方法；在现实生活中，它还为我们解决实际问题提供了重要的思路和启示。因此，让我们继续深入探究双曲线顶点坐标的奥秘和魅力吧！在这个充满挑战与机遇的数学世界中不断前行、不断成长！