如何计算直角三角形的斜边长度

直角三角形斜边计算方法详解

在直角三角形中，斜边是连接直角顶点与另外两个顶点之间的最长边。求解直角三角形的斜边长度是数学和工程计算中的常见问题。本文将详细介绍几种求解直角三角形斜边长度的方法，包括勾股定理、三角函数以及特殊直角三角形的情况。

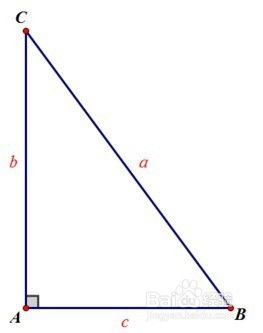
一、勾股定理

勾股定理是求解直角三角形斜边长度的最基本且最常用的方法。该定理表明，在一个直角三角形中，直角两边的平方和等于斜边的平方。用数学公式表示就是：

c² = a² + b²

其中，c 是斜边的长度，a 和 b 分别是直角三角形的两条直角边的长度。

示例：

假设直角三角形的两条直角边长度分别为 3 和 4，则斜边的长度可以通过以下步骤计算：

c² = 3² + 4²

c² = 9 + 16

c² = 25

c = √25

c = 5

因此，斜边的长度为 5。

二、三角函数

三角函数是另一种求解直角三角形斜边长度的方法。在直角三角形中，正弦（sin）、余弦（cos）和正切（tan）等三角函数可以帮助我们找到斜边的长度。

1. 正弦函数：sin(θ) = 对边/斜边

如果我们知道直角三角形的一个锐角 θ 和对应的对边长度，则可以通过正弦函数求解斜边长度：

c = a / sin(θ)

其中，a 是对边长度，θ 是对应的锐角。

2. 余弦函数：cos(θ) = 邻边/斜边

如果我们知道直角三角形的一个锐角 θ 和对应的邻边长度，则可以通过余弦函数求解斜边长度：

c = b / cos(θ)

其中，b 是邻边长度，θ 是对应的锐角。

3. 正切函数：tan(θ) = 对边/邻边

虽然正切函数本身不直接给出斜边的长度，但我们可以利用它找到直角边之间的关系，再结合勾股定理或其他三角函数求解斜边。

示例：

假设直角三角形的一个锐角为 30°，对应的对边长度为 3，则斜边的长度可以通过正弦函数计算：

sin(30°) = 3/c

c = 3 / sin(30°)

c = 3 / (1/2)

c = 6

但需要注意的是，这里的计算是基于 30°-60°-90°特殊直角三角形的情况，因为 sin(30°) = 1/2。在一般情况下，我们需要使用计算器来求解三角函数值。

三、特殊直角三角形

对于某些特殊类型的直角三角形，我们可以直接利用已知的边长比例来求解斜边长度。

1. 30°-60°-90°直角三角形：

在 30°-60°-90°直角三角形中，边长比例是 1:√3:2。其中，较短的直角边（对应 30° 角）与斜边的比例是 1:2，较长的直角边（对应 60° 角）与斜边的比例是 √3:2。

示例：

如果较短的直角边长度为 3，则斜边的长度为：

c = 2 × 3

c = 6

2. 45°-45°-90°直角三角形：

在 45°-45°-90°直角三角形中，两条直角边的长度相等，且都与斜边的长度构成 √2:2 的比例关系。

示例：

如果两条直角边的长度都是 4，则斜边的长度为：

c = 4 × √2

c = 4√2

四、实际应用

求解直角三角形斜边长度的方法在工程和日常生活中有着广泛的应用。例如：

1. 建筑设计：在建筑设计中，我们需要计算建筑物的高度、宽度等尺寸，这些尺寸往往涉及到直角三角形的斜边长度。

2. 电子工程：在电子工程中，信号的传输路径往往可以看作直角三角形的斜边，因此我们需要计算这些路径的长度来评估信号的传输时间和损耗。

3. 物理学：在物理学中，许多运动问题可以简化为直角三角形的模型，例如斜抛运动中的射程和高度等。

五、总结

求解直角三角形斜边长度的方法有多种，包括勾股定理、三角函数以及特殊直角三角形的情况。在实际应用中，我们需要根据问题的具体情况选择合适的方法。勾股定理是最基本且最常用的方法，适用于所有直角三角形；三角函数则提供了更灵活的选择，可以根据已知条件求解斜边长度；而特殊直角三角形则适用于某些特定的情况，可以简化计算过程。

通过掌握这些方法，我们可以更加高效地解决与直角三角形斜边长度相关的问题，为数学学习和实际应用提供有力的支持。