探索无穷大与无界的奥秘
在数学这片浩瀚无垠的宇宙中,有两个令人着迷却又常常令人困惑的概念——无穷大与无界。它们如同夜空中最遥远的星辰,既璀璨夺目,又难以捉摸。今天,就让我们一起踏上这场探索之旅,揭开这两个神秘概念的面纱,看看它们究竟是何方神圣,又如何在我们的数学世界中发挥着举足轻重的作用。

首先,让我们从无穷大说起。在数学中,无穷大(Infinity)通常用符号“∞”来表示,它代表着一个无法被具体量化、超出所有有限数值的极限状态。当我们说某个函数在某一点或某个方向上趋向于无穷大时,意味着该函数的值会随着自变量的变化而无限增大,以至于没有任何有限数能够限制它。

然而,无穷大并非一个具体的数,而是一个描述性的概念。它告诉我们,在某个特定的情境下,某个量在增长的过程中没有上限。这种描述方式在数学分析中尤为关键,因为它允许我们处理那些在某些点或区间内无法被有限数值所约束的函数。例如,在探讨反比例函数y=1/x时,我们会发现当x趋近于0时,y的值会趋向于无穷大。这意味着,尽管我们无法给出一个具体的数值来描述y在x=0时的状态,但我们可以通过无穷大这个概念来理解y值的增长趋势。

接下来,让我们转向无界(Unbounded)的概念。在数学中,一个函数或数列被称为无界的,如果它不存在一个有限的上界或下界。也就是说,无论我们选取多大的正数M作为界限,总能在函数的定义域或数列中找到一个元素,使得其值大于M或小于-M。与无穷大不同,无界强调的是在某个范围内无法找到一个有限的界限来约束函数或数列的值。

举个例子,考虑函数f(x)=x^2。这个函数在实数范围内是无界的,因为对于任意大的正数M,我们总能找到一个实数x(例如x=√M+1),使得f(x)>M。同样地,对于任意小的负数-M,我们也能找到一个实数x(例如x=-√M-1),使得f(x)<-M。因此,f(x)=x^2的值域在实数范围内没有上下界,是一个无界的函数。
现在,让我们深入探讨一下无穷大与无界之间的关系。虽然这两个概念在数学中都用于描述某种形式的“无限”,但它们之间却存在着微妙的差异。首先,无穷大是一个具体的极限状态,它描述了一个函数或数列在某个特定点或方向上的增长趋势。而无界则是一个更宽泛的概念,它关注的是函数或数列在其定义域或值域内是否存在一个有限的界限来约束其值。
具体来说,一个趋向于无穷大的函数一定是无界的,但一个无界的函数并不一定趋向于无穷大。这是因为无界只要求函数或数列在其定义域或值域内没有有限的界限,而不关心它是否在某个特定点或方向上趋向于无穷大。例如,考虑函数f(x)=(-1)^x*x。这个函数在整数范围内是无界的,因为无论我们选取多大的正数M,总能在整数集中找到一个数x,使得f(x)的绝对值大于M。然而,这个函数并不趋向于无穷大,因为它的值在正负无穷大之间振荡。
此外,值得注意的是,在数学分析中,无穷大与无界的概念通常与极限理论紧密相连。当我们讨论一个函数在某点或某方向上的极限时,无穷大和无界的概念常常成为我们判断极限是否存在以及极限值大小的重要依据。例如,在洛必达法则中,我们就需要判断分子和分母在极限点处的增长趋势(即是否趋向于无穷大)来确定极限值是否存在以及其具体大小。
除了在数学分析中的应用外,无穷大与无界的概念还在其他数学分支中发挥着重要作用。例如,在复变函数中,无穷远点被视为复平面上的一个特殊点,它与无穷大的概念紧密相连。在拓扑学中,无界的概念被用于描述空间的某种“无限性”特征,从而帮助我们理解空间的拓扑结构和性质。
当然,无穷大与无界的概念也引发了哲学家和数学家们的深入思考和讨论。他们试图探究这些概念在数学中的本质意义以及它们与现实世界的联系。例如,康托尔(Cantor)等数学家通过集合论的方法对无穷大的概念进行了深入的研究和探讨,从而为我们理解无穷大的本质提供了更为深刻的视角。
最后,值得一提的是,尽管无穷大与无界的概念在数学中具有重要的地位和作用,但我们在实际应用中也需要谨慎对待它们。因为这两个概念都涉及到某种形式的“无限”,所以在处理实际问题时我们需要确保所使用的方法和结论在有限的范围内是有效和可靠的。同时,我们也需要保持对这两个概念的敬畏之心,因为它们所描述的“无限”状态远远超出了我们日常生活中的经验和认知范围。
综上所述,无穷大与无界是数学中两个既神秘又迷人的概念。它们不仅在数学分析中发挥着举足轻重的作用,还在其他数学分支以及哲学思考中扮演着重要的角色。通过深入探究这两个概念的本质意义和应用范围,我们可以
- 上一篇: 火灾发生后如何准确报火警
- 下一篇: 揭秘:原耽信息素到底是什么?
-
 输入正无穷符号的方法资讯攻略02-21
输入正无穷符号的方法资讯攻略02-21 -
 揭秘!在不夜星球边缘,如何巧妙激活隐形模式,探索未知无界资讯攻略10-24
揭秘!在不夜星球边缘,如何巧妙激活隐形模式,探索未知无界资讯攻略10-24 -
 如何设置链在一起软件的中文汉化?资讯攻略10-23
如何设置链在一起软件的中文汉化?资讯攻略10-23 -
 《剑网3无界》独家揭秘:一键直达兑换码输入宝地,福利领取不迷路!资讯攻略10-23
《剑网3无界》独家揭秘:一键直达兑换码输入宝地,福利领取不迷路!资讯攻略10-23 -
 无穷大的标准符号是什么资讯攻略11-27
无穷大的标准符号是什么资讯攻略11-27 -
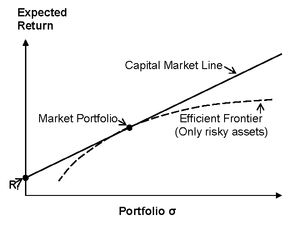 揭秘:风险溢价计算的奥秘公式资讯攻略11-18
揭秘:风险溢价计算的奥秘公式资讯攻略11-18











