互质数：详细解析与定义

互质数：数学世界的奇妙概念

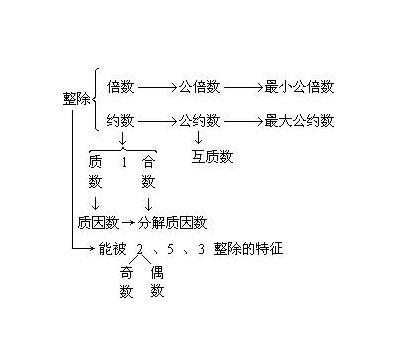
在数学的浩瀚宇宙中，互质数犹如璀璨星辰，它们独特而神秘，激发着无数数学家和爱好者的探索欲望。那么，互质数究竟是什么意思呢？本文将为您深入解读这一概念，揭示其背后的数学奥秘。

互质数，简而言之，是指两个或多个整数的公因数只有1的非零自然数。这意味着，如果我们有两个数a和b，它们除了1以外没有其他共同的因数，那么我们就可以说a和b是互质数。例如，2和3就是一对互质数，因为它们的公因数只有1。

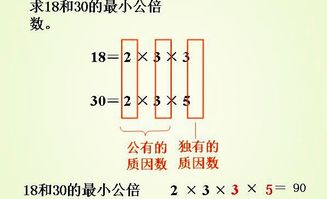
互质数的概念在数学中具有重要的地位。它不仅与分数的简化、密码学、整数分解等领域有着紧密的关联，还蕴含着许多深刻的数学原理和实际应用。

首先，让我们从分数的简化说起。在简化分数时，我们通常要找到分子和分母的最大公约数（GCD），并将其约去。而互质数正是那些最大公约数为1的数对，因此，如果分子和分母是互质数，那么这个分数就已经是最简形式了。这为我们提供了一种快速判断分数是否已简化的方法。

接下来，让我们看看互质数在密码学中的应用。在RSA加密算法中，两个大素数的乘积被用于加密和解密。而这两个大素数必须满足互质的条件。这是因为，如果两个数不是互质的，那么它们就存在共同的因数，这可能会使得加密算法变得不安全。因此，在选择素数时，我们必须确保它们是互质的。这体现了互质数在密码学中的重要作用。

此外，互质数还与整数分解有着密切的联系。整数分解是数论中的一个重要问题，它涉及到将一个整数表示为若干个素数的乘积。而互质数的概念则为我们提供了一种分解整数的方法。例如，如果我们知道两个互质的数a和b的乘积c，那么我们就可以通过寻找a和b的因数来分解c。虽然这种方法并不总是有效，但在某些情况下，它可以为我们提供一些有用的线索。

除了以上应用外，互质数还具有许多有趣的性质和判定方法。以下是一些常见的互质数判定方法：

1. 两个质数一定是互质数。例如，2与7、13与19都是互质数。这是因为质数只有两个因数：1和它本身。因此，任何两个不同的质数都只能有1作为公因数。

2. 一个质数如果不能整除另一个合数，这两个数为互质数。例如，3与10、5与26都是互质数。这是因为，如果一个质数不能整除一个合数，那么它们之间就不可能有除了1以外的共同因数。

3. 1不是质数也不是合数，它和任何一个自然数在一起都是互质数。例如，1和9908是互质数。这是因为1是所有数的因数，但它本身并没有除了1以外的因数，所以它和任何数都只能有1作为公因数。

4. 相邻的两个自然数是互质数。例如，15与16是互质数。这是因为相邻的两个自然数之间不可能有除了1以外的共同因数。

5. 相邻的两个奇数是互质数。例如，49与51是互质数。这是因为相邻的两个奇数之间也不可能有除了1以外的共同因数。

6. 大数是质数的两个数是互质数。例如，97与88是互质数。这是因为如果大数是质数，那么它只能被1和它本身整除，所以它和任何小于它的数都只能有1作为公因数。

7. 小数是质数，大数不是小数的倍数的两个数是互质数。例如，7和16是互质数。这是因为如果小数是质数，而大数不是小数的倍数，那么它们之间就不可能有除了1以外的共同因数。

8. 两个数都是合数（二数差又较大），小数所有的质因数，都不是大数的约数，这两个数是互质数。例如，357与715是互质数。这是因为357的所有质因数（3、7、17）都不是715的约数。

9. 两个数都是合数（二数差较小），这两个数的差的所有质因数都不是小数的约数，这两个数是互质数。例如，85和78是互质数。因为85-78=7，而7不是78的约数。

10. 两个数都是合数，大数除以小数的余数（不为“0”且大于“1”）的所有质因数，都不是小数的约数，这两个数是互质数。例如，462与221是互质数。因为462÷221=2余20