合数、约数、质数、素数定义详解

在数学的世界里，有几个基础而重要的概念，它们分别是合数、约数、质数和素数。这些概念不仅是学习数学的基础，而且在日常生活中也有广泛的应用。接下来，让我们一起深入探讨这些概念。

首先，我们来看合数。合数是一个大于1的自然数，它不是质数。换句话说，一个合数除了1和它本身以外，还有其他因数。例如，数字6就是一个合数，因为它可以被2和3整除，而2和3都是6的因数，且既不是1也不是6本身。再举一个例子，数字28也是一个合数，它的因数包括1、2、4、7、14和28，其中2、4、7、14都是除了1和28以外的因数。从这两个例子中，我们可以看出，合数的一个重要特征是它有多个因数。

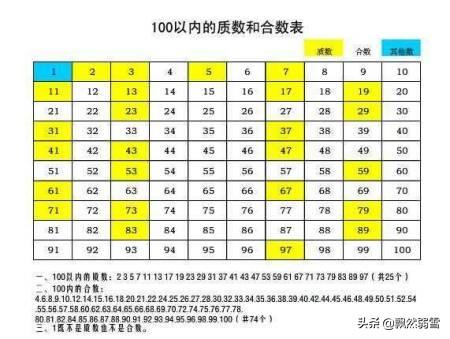
与合数相对的是质数和素数（在数学中，质数和素数通常被视为同一个概念，即一个大于1的自然数，除了1和它本身以外不再有其他因数）。为了深入理解合数，我们先来理解质数和素数的概念。质数是一个大于1的自然数，它只有两个正因数：1和它本身。例如，数字2是质数，因为它只有两个因数：1和2。同样，数字3、5、7、11、13等都是质数，因为它们都只有两个因数。质数在数论中扮演着非常重要的角色，它们是构成所有自然数的基础单元。在日常生活和科学技术中，质数也有广泛的应用，比如加密技术和通信安全。

现在我们再回到合数的概念。由于合数有多个因数，因此它可以通过其他自然数的乘积来表示。例如，数字6可以表示为2和3的乘积，数字28可以表示为2的平方和7的乘积。这种通过乘积表示合数的方法在数学中被称为合数的因数分解。因数分解是数学中的一个重要技能，它可以帮助我们解决各种问题，比如求最大公约数和最小公倍数。

接下来，我们来看约数的概念。约数是指能够整除一个数的数。例如，对于数字6，它的约数包括1、2、3和6，因为这些数都能整除6而不留余数。同样，对于数字28，它的约数包括1、2、4、7、14和28。从这两个例子中，我们可以看出，一个数的约数包括它本身和1，以及所有能整除它的正整数。如果一个数有多个约数（除了1和它本身以外），那么这个数就是合数；如果一个数只有两个约数（1和它本身），那么这个数就是质数（或素数）。

现在我们已经了解了合数、质数（素数）和约数的基本概念，接下来我们来探讨它们之间的关系和性质。首先，一个自然数要么是质数，要么是合数，要么是1（在数学中，1通常被视为既不是质数也不是合数的特殊数）。这个性质被称为自然数的分类性质。通过分类性质，我们可以将自然数划分为三个不同的集合：质数集合、合数集合和1的集合。

其次，质数和合数之间有一些重要的性质。例如，质数是无限多的，这意味着无论我们找到多少个质数，总会有更多的质数存在。这个性质被称为质数的无穷性。质数的无穷性在数学中有许多重要的应用，比如证明某些数学定理和构造特殊的数学对象。另外，质数之间还有一些有趣的分布规律，比如素数定理和哥德巴赫猜想等。这些规律和猜想都是数学研究的重要课题之一。

与质数相比，合数的性质更加复杂多样。由于合数有多个因数，因此它们可以通过不同的方式进行因数分解。这种多样性使得合数在数学中有许多不同的应用。例如，在密码学中，合数的因数分解问题被用来构建安全的加密算法；在组合数学中，合数的性质被用来解决各种排列组合问题；在数论中，合数的分布规律被用来研究自然数的结构和性质等。

最后，我们来看约数与质数、合数之间的关系。对于一个质数来说，它的约数只有两个：1和它本身。这意味着质数在约数方面是非常“简单”的。而对于一个合数来说，它的约数则不止两个，这使得合数在约数方面更加“复杂”。然而，正是这种复杂性使得合数在数学中有更多的应用机会和更丰富的性质表现。

此外，约数还与数学中的其他概念密切相关。例如，最大公约数和最小公倍数都是通过约数来定义的。最大公约数是指两个或多个整数共有的最大的约数；最小公倍数则是指能够同时被这些整数整除的最小的数。通过利用约数的性质，我们可以方便地求出两个或多个整数的最大公约数和最小公倍数。

总的来说，合数、约数、质数和素数是数学中非常基础而重要的概念。它们不仅在数学学科内部有着广泛的应用和深入的研究，而且在日常生活和科学技术中也有着重要的价值和意义。通过理解和掌握这些概念及其性质和关系，我们可以更好地理解和应用数学知识，为解决各种问题提供更加有效的工具和方法。因此，我们应该重视这些基础概念的学习和研究，不断提高自己的数学素养和能力水平。