揭秘三角形的核心概念与独特性质
探索三角形的奥秘:从概念到性质的奇妙之旅

在我们生活的这个多彩多姿的世界里,三角形无处不在。从宏伟的埃菲尔铁塔到精致的建筑门窗,从桥梁的坚固构造到自然界中蜂巢的六边形排列(虽然直接提到的是六边形,但每个六边形由三个三角形组成,这也是三角形应用的一个巧妙例证),三角形以它独有的魅力,默默支撑着这个世界的稳定与和谐。今天,就让我们一同踏上这场探索之旅,揭开三角形的神秘面纱,深入了解它的概念和性质,发现那些隐藏在日常生活中的数学之美。

三角形的概念:几何的基石
想象一下,当你用三根长度各异的木棒尝试首尾相接时,一个奇妙的图形悄然诞生——三角形。在数学的世界里,三角形被定义为由三条直线(或称为边)相交连接而成的封闭图形,且这三条直线中的任意两条都不在同一直线上。三角形的这一简单定义,却蕴含着无尽的智慧与奥秘。

三角形的三个顶点,如同三位亲密无间的朋友,它们之间的距离(即边长)决定了三角形的形状和大小。而连接这三个顶点的三条边,则是三角形稳定的基石,正是这三条边的相互支撑,使得三角形成为了几何图形中最稳定的结构之一。
三角形的分类:多样的形态
三角形,这个看似简单的几何图形,实则拥有着千变万化的形态。根据边长和角度的不同,我们可以将三角形分为以下几类:
1. 等边三角形:三条边等长,三个角均为60度的三角形。它是三角形中最完美的形态,每一边都扮演着相同的角色,每一个角都散发着均衡的美感。
2. 等腰三角形:有两条边等长的三角形。它像是一位优雅的舞者,在保持稳定的同时,又不失灵活与变化。等腰三角形的两个底角相等,这是它独特的标志。
3. 不等边三角形:三条边各不相等的三角形。它是三角形中最常见的形态,每一条边、每一个角都独一无二,如同大千世界中每一个独一无二的生命。
此外,我们还可以根据角度对三角形进行分类:锐角三角形(所有角均小于90度)、直角三角形(有一个角为90度)和钝角三角形(有一个角大于90度)。每一种类型的三角形,都在以它独有的方式,诠释着几何学的魅力。
三角形的性质:稳定的奥秘
三角形之所以能够在众多几何图形中脱颖而出,成为稳定的代名词,得益于它一系列独特的性质。
1. 稳定性:三角形的稳定性是其最显著的性质之一。在物理学中,一个物体要想保持稳定,必须满足一定的力学条件。而三角形,凭借其三条边相互支撑的结构,使得它在受到外力作用时,能够保持形状的不变,从而实现了稳定。这也是为什么在建筑、桥梁等工程中,三角形结构被广泛应用的原因。
2. 内角和定理:三角形的三个内角之和等于180度。这是三角形最基本的性质之一,也是几何学中最基本的定理之一。这个定理不仅揭示了三角形角度之间的关系,还为后续解决复杂的几何问题提供了有力的工具。
3. 边与角的关系:在三角形中,边与角之间存在着密切的关系。例如,在任意三角形中,大边对大角,小边对小角。这一性质,使得我们可以通过观察三角形的边长或角度,来推断出三角形的其他性质。
4. 三角形的中线、高、垂直平分线和角平分线:这些特殊的线段,不仅丰富了三角形的几何性质,还为解决三角形的相关问题提供了更多的方法和思路。例如,三角形的中线将对应的底边平分,且与对应的顶点相连形成的两条线段长度相等;三角形的高,则是从三角形的一个顶点垂直到对边或对边的延长线所形成的线段,它揭示了三角形面积与边长之间的关系。
5. 三角形的面积公式:三角形的面积可以通过多种公式来计算,其中最常见的是海伦公式和底乘高公式。海伦公式通过三角形的三边长来计算面积,而底乘高公式则是通过三角形的底边和高来计算面积。这些公式不仅为计算三角形的面积提供了便捷的方法,也揭示了三角形边长、角度与面积之间的内在联系。
三角形的应用:生活中的数学之美
三角形,这个看似抽象的几何图形,其实与我们的生活息息相关。在建筑领域,三角形结构被广泛应用于桥梁、塔吊、房屋等建筑中,以提高其稳定性和承重能力。在艺术创作中,三角形作为构图的基本元素之一,被艺术家们巧妙地运用在绘画、雕塑等作品中,以营造出独特的视觉效果和审美体验。在自然界中,三角形的身影同样无处不在。从蜂巢的六边形排列到树叶的脉络分布,从动物的骨骼结构到植物的根系生长,三角形都在以它独有的方式,诠释着自然界的奥秘和规律。
结语:探索未尽,魅力永恒
三角形,这个简单而又神奇的几何图形,以其独特的概念和性质,吸引着无数数学家、物理学家、工程师和艺术家去探索、去研究、去创造。从古老的埃及金字塔到现代的摩天大楼,从古老的几何学著作到现代的数学研究,三角形都在以它
- 上一篇: 解析:万事顺意与万事胜意的核心差异
- 下一篇: 个人征信官网查询方法
-
 揭秘反函数:一图看懂其核心概念资讯攻略11-18
揭秘反函数:一图看懂其核心概念资讯攻略11-18 -
 直角三角形斜边求解方法资讯攻略11-16
直角三角形斜边求解方法资讯攻略11-16 -
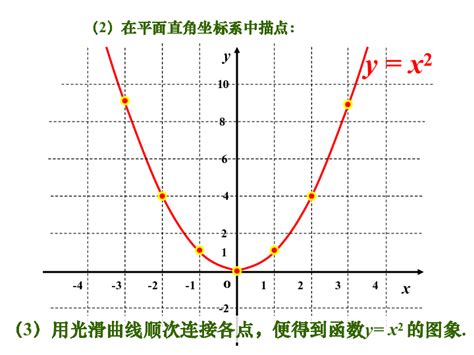 深入解析二次函数图像及其核心性质资讯攻略10-29
深入解析二次函数图像及其核心性质资讯攻略10-29 -
 揭秘!原子与分子的核心差异究竟在哪?资讯攻略12-06
揭秘!原子与分子的核心差异究竟在哪?资讯攻略12-06 -
 揭秘正方形对角线的神奇性质资讯攻略12-01
揭秘正方形对角线的神奇性质资讯攻略12-01 -
 揭秘!你真的了解‘仪器’这个概念吗?资讯攻略10-27
揭秘!你真的了解‘仪器’这个概念吗?资讯攻略10-27












