揭秘反函数:一图看懂其核心概念
在数学的广阔天地里,反函数是一个既基础又重要的概念,它为我们提供了一种独特的视角去审视和理解函数之间的关系。直观了解反函数的相关知识,不仅能够帮助我们深化对函数本质的认识,还能在解决实际问题时提供有力的工具。以下,我们将从多个维度深入探讨反函数,包括其定义、性质、存在条件、求解方法以及在实际问题中的应用,旨在为您呈现一个全面而直观的反函数知识体系。
首先,明确反函数的定义至关重要。简单来说,如果函数f将集合A中的元素x映射到集合B中的元素y,即f(x)=y,那么存在一个函数g,能够将集合B中的元素y映射回集合A中的元素x,即g(y)=x,且这种映射是唯一的,那么函数g就被称为函数f的反函数。值得注意的是,反函数的存在依赖于原函数在其定义域内的单调性,这是保证反函数唯一性的关键。

接下来,我们探讨反函数的一些基本性质。首先,反函数的定义域是原函数的值域,反函数的值域是原函数的定义域。这一性质直接体现了反函数与原函数之间的互逆关系。其次,如果函数f在某区间内单调增加(或减少),则其反函数在该区间内也单调增加(或减少)。这意味着,原函数与反函数在单调性上保持一致。此外,如果函数f在其定义域内连续且单调,则其反函数也在其值域内连续。这些性质为我们理解和应用反函数提供了重要的依据。
那么,什么样的函数存在反函数呢?如前所述,函数的单调性是决定其是否存在反函数的关键因素。具体来说,如果一个函数在其定义域内的任意两点x1和x2(x1f(x2)),则称该函数在该区间内单调增加(或减少)。只有这样的函数,才能保证每一个y值在值域内只对应一个x值,从而存在唯一的反函数。因此,当我们判断一个函数是否存在反函数时,首先需要检查该函数是否在其定义域内单调。
求解反函数的过程,实际上是一个逆向操作的过程。给定一个函数f(x),我们需要找到其反函数f^(-1)(y)。具体步骤如下:首先,将f(x)的表达式中的x和y互换位置,得到y=f(x)的等价形式;然后,解这个等式以y为未知数,得到x关于y的表达式;最后,将x和y换回原来的符号,即得到反函数f^(-1)(y)的表达式。需要注意的是,在求解过程中,我们需要确保解得的表达式满足反函数的定义,即它是唯一的且定义在f的值域上。
反函数在实际问题中的应用广泛而多样。在经济学中,反需求函数帮助我们理解价格与需求量之间的关系,从而制定有效的市场策略。在物理学中,反函数常用于解决逆运动学问题,如确定物体的运动轨迹。在工程学中,反函数被广泛应用于优化设计、控制系统等领域。此外,在数据分析、图像处理、信号处理等领域,反函数也发挥着重要作用。这些应用实例充分展示了反函数作为数学工具的重要性和实用性。
为了更直观地理解反函数,我们可以通过一些具体的例子进行说明。例如,考虑函数f(x)=2x+3。这是一个线性函数,在实数范围内单调增加。因此,它存在反函数。按照求解反函数的步骤,我们首先交换x和y的位置得到y=2x+3;然后解这个等式以y为未知数得到x=(y-3)/2;最后将x和y换回原来的符号得到反函数f^(-1)(y)=(y-3)/2。通过这个例子,我们可以清晰地看到反函数与原函数之间的互逆关系以及求解反函数的过程。
另外,值得注意的是,并非所有函数都存在反函数。例如,函数f(x)=x^2在实数范围内就不存在反函数,因为对于每一个正数y值,都存在两个x值(一个正数和一个负数)使得f(x)=y。这种情况下,我们称函数f(x)不是单射的,即其值域中的元素与定义域中的元素不是一一对应的。因此,在判断一个函数是否存在反函数时,我们需要仔细分析其单调性和值域。
最后,我们来谈谈反函数在微积分中的应用。在微积分中,反函数的导数(即反导数)具有特殊的性质。具体来说,如果函数f(x)在其定义域内单调且可导,则其反函数f^(-1)(y)也在其值域内可导,并且它们的导数之间满足关系式[f^(-1)]'(y)=1/f'(x),其中x=f^(-1)(y)。这一性质在求解某些类型的积分问题时非常有用。例如,当我们需要求解形如∫1/f'(x)dx的积分时,如果f(x)存在反函数且容易求出,那么我们就可以利用反函数的导数性质将其转化为关于反函数的积分问题,从而简化求解过程。
综上所述,反函数作为数学中的一个基本概念,具有广泛的应用价值和重要的理论意义。通过深入学习和理解反函数的定义、性质、存在条件、求解方法以及在实际问题中的应用,我们可以更加灵活地运用这一数学工具去解决各种复杂问题。同时,这也将为我们进一步探索数学的奥秘奠定坚实的基础。
- 上一篇: 轻松学会!蜈蚣辫简易扎法图解,让你爱不释手
- 下一篇: 如何在YY软件中创建频道?
-
 一图看懂:自动挡汽车档位全面解析资讯攻略11-30
一图看懂:自动挡汽车档位全面解析资讯攻略11-30 -
 揭秘导数概念:一文读懂资讯攻略12-04
揭秘导数概念:一文读懂资讯攻略12-04 -
 轻松学会!如何看懂简谱?资讯攻略12-06
轻松学会!如何看懂简谱?资讯攻略12-06 -
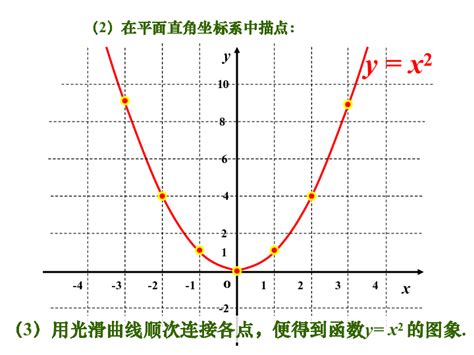 深入解析二次函数图像及其核心性质资讯攻略10-29
深入解析二次函数图像及其核心性质资讯攻略10-29 -
 云顶之弈11.3秘术摄魂使大揭秘:你不得不知的顶尖玩法与阵容搭配,一次看懂!资讯攻略11-08
云顶之弈11.3秘术摄魂使大揭秘:你不得不知的顶尖玩法与阵容搭配,一次看懂!资讯攻略11-08 -
 log函数的导数如何求解?资讯攻略11-10
log函数的导数如何求解?资讯攻略11-10












