无理数的定义与解释

探索数学奥秘：揭开无理数的神秘面纱

在数学这片广袤而深邃的领域里，有一类数字既不像整数那样直白明了，也不像分数那样可以精确表达，它们就是充满神秘色彩的无理数。当你听到“无理数”这个词汇时，是否心中充满了疑惑和好奇？今天，就让我们一同踏上探索之旅，揭开无理数的神秘面纱，看看它们究竟是何方神圣，为何会让众多数学家和数学爱好者为之着迷。

一、初识无理数：定义与特性

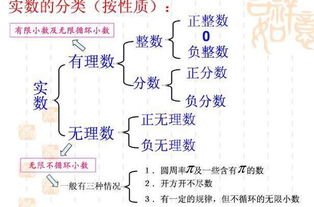
在数学的大家庭中，数字被分为有理数和无理数两大类。有理数，顾名思义，就是可以表示为两个整数之比的数，比如1/2、3/4等。而无理数，则无法表示为两个整数的比，它们的小数部分是无限不循环的。这种特性使得无理数在形式上显得尤为独特和复杂。

提到无理数，我们不得不提几个著名的例子：圆周率π和自然对数的底数e。这两个数在数学中无处不在，却又无法精确表示。π的值大约为3.141592653589793...，而e的值大约为2.718281828459045...。这两个数的小数部分永远不会结束，也永远不会循环，这就是无理数的典型特征。

二、无理数的发现：历史与争议

无理数的发现，是数学史上的一次重大突破，也是一次充满争议的变革。早在古希腊时期，数学家们就开始了对有理数和无理数的研究。然而，无理数的出现却引发了极大的争议和困惑。

当时，毕达哥拉斯学派认为，宇宙间的一切都可以用有理数来表示。然而，当他们的学生希帕索斯发现正方形对角线与边长之比无法表示为有理数时，这一观点遭到了严峻的挑战。希帕索斯的发现，即现在所说的根号2是无理数，彻底打破了毕达哥拉斯学派的传统观念，引发了数学界的轩然大波。

无理数的存在，让数学家们开始重新审视有理数和无理数的关系，推动了数学的发展。尽管当时无理数的概念并未被广泛接受，但随着时间的推移，数学家们逐渐认识到了无理数的重要性，并将其纳入了数学的范畴。

三、无理数的应用：无处不在的奇妙

无理数不仅在数学领域有着举足轻重的地位，还在现实生活中发挥着重要作用。它们的存在，让我们的生活变得更加丰富多彩和充满乐趣。

在几何学中，无理数扮演着至关重要的角色。比如，圆的周长与直径之比π就是一个无理数。正是因为π的存在，我们才能计算出圆的周长和面积，进而解决各种与圆相关的几何问题。同样地，在三角形的内角和为180度这一定理中，也隐藏着无理数的身影。虽然这个定理的表述并不直接涉及无理数，但在证明过程中，我们往往需要用到与无理数相关的知识和技巧。

在物理学中，无理数同样有着广泛的应用。比如，在描述简谐振动和波动现象时，我们经常会用到自然对数的底数e和圆周率π。这两个无理数的存在，使得我们能够更准确地描述和预测物理现象的变化规律。

此外，在计算机科学中，无理数也发挥着重要作用。比如，在图形处理和计算机图形学中，我们经常需要用到浮点数来表示各种数值。而浮点数的精度和表示范围，往往与无理数的小数位数和性质密切相关。因此，对于无理数的研究和应用，对于推动计算机科学的发展也具有重要意义。

四、无理数的魅力：挑战与探索

无理数的魅力，不仅在于它们的独特性和复杂性，更在于它们所带来的挑战和探索的乐趣。对于数学家和数学爱好者来说，无理数就像是一个充满未知的神秘世界，等待着我们去探索和发现。

首先，无理数的小数部分是无限不循环的，这使得我们无法直接精确表示它们的值。然而，正是这种不确定性，激发了数学家们对于无理数研究的热情和兴趣。他们通过各种方法，如近似计算、级数展开等，来逼近无理数的值，从而更深入地了解它们的性质和特点。

其次，无理数在数学中与其他概念的关联和相互作用，也为我们提供了丰富的探索空间。比如，无理数与有理数之间的界限和关系，无理数与实数轴上的点之间的对应关系，以及无理数在复数域中的表现等，都是值得深入研究和探讨的问题。

最后，无理数在现实生活中的广泛应用，也为我们提供了更多的实践机会和探索空间。比如，在工程设计、金融分析等领域中，我们经常需要用到无理数来进行精确计算和预测。这些应用不仅加深了我们对无理数的理解和掌握，也推动了相关领域的发展和进步。

五、结语：走进无理数的奇妙世界

无理数，这个看似简单却又充满神秘的数学概念，一直以来都吸引着无数数学家和数学爱好者的目光。通过探索无理数的定义、特性、历史、应用以及魅力等方面，我们不仅加深了对数学这门学科的认识和理解，也感受到了数学