解密有理数:轻松理解有理数的含义
在数学的浩瀚宇宙中,有一个基础而重要的概念如同星辰般璀璨,它贯穿了算术、代数乃至更高级别的数学领域,那便是“有理数”。有理数,这一简洁明了的术语,实则蕴含着丰富的数学内涵与广泛的应用场景。本文将从定义解析、历史渊源、性质探讨、实际应用以及与其他数集的关联等多个维度,深入浅出地阐述什么是有理数。

定义解析:有理数的本质
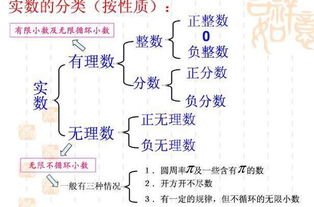
首先,我们直接切入主题,探讨有理数的定义。有理数,顾名思义,即“可以表示为两个整数的比的数”,这里要求分母不为零。用数学符号表示即为:如果存在整数a和b(b≠0),使得x=a/b,则称x为有理数。这个定义简单而直观,但它揭示了有理数的两大构成要素:分子(整数a)和分母(非零整数b)。通过这两个整数的比值,我们可以表示出无限多个有理数,包括但不限于正整数、负整数、正分数、负分数以及零(可视为0/1或任意非零数与自身的比值)。

历史渊源:有理数的起源与发展
追溯有理数的历史,我们可以回到古希腊时代。在那个数学与哲学交织的辉煌时期,毕达哥拉斯学派提出了“万物皆数”的哲学观点,并致力于探索数与几何的奥秘。然而,当该学派成员希帕索斯发现了根号2不能表示为两个整数的比时,这一发现动摇了学派的基础信仰,引发了第一次数学危机。根号2的发现,实际上揭示了有理数集之外还有更为广阔的无理数世界,但这也促使了有理数概念的形成与明确。此后,数学家们逐渐认识到,能够精确表示为两个整数之比的数是一类特殊的数,即有理数。

性质探讨:有理数的独特魅力
有理数不仅定义明确,而且具备一系列独特的数学性质,这些性质使得有理数在数学体系中占据了举足轻重的地位。
1. 封闭性:有理数集在加、减、乘、除(除数不为零)运算下是封闭的,即任意两个有理数经过这些运算后,结果仍然是有理数。
2. 稠密性:在有理数集中,任意两个有理数之间都存在无数个有理数。这种性质使得有理数在数轴上分布得极为紧密,几乎填满了整个数轴(但实际上,由于无理数的存在,数轴并非完全由有理数填满)。
3. 有序性:有理数集可以按照大小进行排序,满足传递性、反身性和比较性,这使得有理数之间可以进行大小比较和排序操作。
4. 数轴表示:每一个有理数都可以在数轴上找到唯一的点与之对应,反之亦然。这种一一对应的关系加深了我们对有理数直观理解的同时,也为解决实际问题提供了有力的工具。
实际应用:有理数的现实生活意义
有理数不仅仅是一个抽象的数学概念,它在现实生活中有着广泛的应用。从基础的度量衡到复杂的经济模型,有理数都扮演着不可或缺的角色。
度量衡:在日常生活中,我们使用有理数来表示长度、重量、容量等物理量。例如,一本书的重量可能是0.5千克(即500克),这里的0.5就是一个有理数。
财务计算:在财务管理中,有理数被广泛应用于利息计算、汇率转换、成本控制等方面。通过精确的有理数运算,企业可以做出更加科学合理的财务决策。
科学研究:在物理学、化学、生物学等自然科学领域,有理数作为数学工具被广泛应用于实验数据的处理与分析中。通过有理数模型,科学家们能够更准确地描述自然现象的规律与特征。
与其他数集的关联:有理数的位置与角色
在数学的数系结构中,有理数占据了承上启下的关键位置。它上承自然数、整数,下启实数(包括无理数)、复数等更高级别的数集。
自然数与整数:自然数是整数的一部分(不包括负整数),而整数集又是有理数集的一个子集(整数可以视为分母为1的有理数)。这种包含关系体现了数学数系发展的逻辑性和连贯性。
实数与无理数:有理数与无理数共同构成了实数集。尽管有理数在数轴上分布得极为紧密,但它们之间仍然存在着“空隙”,这些空隙就是由无理数填充的。无理数的发现不仅丰富了数系的内涵,也推动了数学理论的深入发展。
综上所述,有理数作为数学中的一个基本概念,不仅具有明确的定义和丰富的性质,而且在现实生活中有着广泛的应用价值。通过深入探讨有理数的定义、历史、性质、应用以及与其他数集的关联,我们可以更加全面地理解这一数学概念的深刻内涵和广泛意义。
-
 有理数的定义及实例解析资讯攻略10-25
有理数的定义及实例解析资讯攻略10-25 -
 实数探秘:全面解析及生动实例资讯攻略11-21
实数探秘:全面解析及生动实例资讯攻略11-21 -
 揭秘!有理数究竟是什么?一文带你彻底搞懂资讯攻略10-26
揭秘!有理数究竟是什么?一文带你彻底搞懂资讯攻略10-26 -
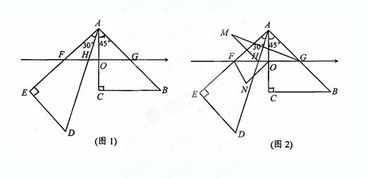 探索数轴:理解数学世界的直线奥秘资讯攻略11-25
探索数轴:理解数学世界的直线奥秘资讯攻略11-25 -
 无理数的定义与解释资讯攻略11-05
无理数的定义与解释资讯攻略11-05 -
 有理化分式的具体方法资讯攻略10-30
有理化分式的具体方法资讯攻略10-30












